
 (1998•山东)如图,在边长为a的正方形ABCD的一边BC上任取一点E,作EF⊥AE交CD于点F,如果BE=x,CF=y,那么用x的代数式表示y是( )
(1998•山东)如图,在边长为a的正方形ABCD的一边BC上任取一点E,作EF⊥AE交CD于点F,如果BE=x,CF=y,那么用x的代数式表示y是( ) 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
 移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.
移动,同时,点Q从点O开始以每秒a(1≤a<3)个单位长度的速度沿射线OB向右移动.设t(0<t≤4)秒后,PQ交OC于点R.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
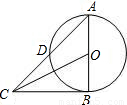
 (1998•山东)已知:如图,AB为⊙O的直径,C是⊙O上一点,过点C的切线与AB的延长线相交于点E,AD⊥EC,垂足为D,且AD交⊙O于点F.
(1998•山东)已知:如图,AB为⊙O的直径,C是⊙O上一点,过点C的切线与AB的延长线相交于点E,AD⊥EC,垂足为D,且AD交⊙O于点F.查看答案和解析>>
科目:初中数学 来源:2009年福建省三明市大田二中自主招生数学模拟试卷(2)(解析版) 题型:选择题
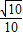
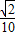
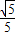
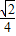
查看答案和解析>>
科目:初中数学 来源:2000年江苏省南通市启东中学高一提前招生试卷(解析版) 题型:选择题
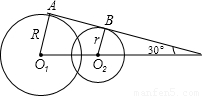
 (R-r)
(R-r)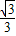 (R-r)
(R-r)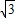 (R-r)
(R-r)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com