
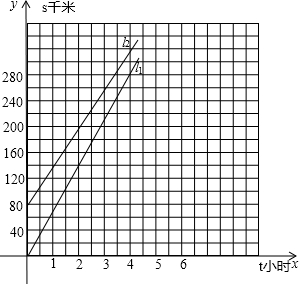
 A、B两车分别在甲、乙两地同时开往丙地,图中l1、l2分别表示两车离甲地的距离与行驶时间之间的关系.
A、B两车分别在甲、乙两地同时开往丙地,图中l1、l2分别表示两车离甲地的距离与行驶时间之间的关系.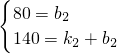 ,140=2k1
,140=2k1 ,k1=70,
,k1=70,

科目:初中数学 来源: 题型:
 A、B两车分别在甲、乙两地同时开往丙地,图中l1、l2分别表示两车离甲地的距离与行驶时间之间的关系.
A、B两车分别在甲、乙两地同时开往丙地,图中l1、l2分别表示两车离甲地的距离与行驶时间之间的关系.查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
查看答案和解析>>
科目:初中数学 来源:双色笔记八年级数学上(北京师大版) 题型:044
甲、乙两地相距600km,快车匀速走完全程需10h,慢车匀速走完全程需15h,两车分别从甲、乙两地同时相向而行.求从出发到相遇两车的距离y(km)与行驶时间x(h)之间的函数关系式,并在坐标系中画出函数的图像.
查看答案和解析>>
科目:初中数学 来源: 题型:044
甲乙两地相距600km,快车匀速走完全程需10h,慢车匀速完全程需15h,两车分别从甲乙两地同时相向而行.求从出发到相遇,两车的距离y(km)与行驶的时间x(h)之间的函数关系式,并指出自变量x的取值范围,在给定的坐标系中画出函数的图像.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com