
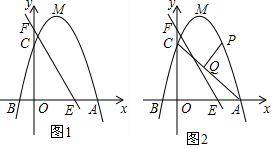
���� ��1���ֱ���x=0��y=0�����������������Ľ������꣬�����䷽������������꼴�ɣ�
��2����ͼ2�У�����P��PN��y�ύAC��N����PQ=$\frac{\sqrt{2}}{2}$PN�����PN�����ֵ���ɣ�
��3������M�䣨1+m��4-2m����A�䣨3+m��-2m����C�䣨m��3-2m��������A��C��2=18��A��P2=��$\frac{3}{2}$+m��2+��2m+$\frac{15}{4}$��2��C��P2=��m-$\frac{3}{2}$��2+��2m+$\frac{3}{4}$��2��
���������Σ����ù��ɶ����г����̼��ɽ�����⣮
��� �⣺��1������������y=-x2+2x+3��
��x=0��y=3�����C���꣨0��3����
��y=0��-x2+2x+3=0�����x=-1��3��
��B��-1��0����A��3��0����
��y=-x2+2x+3=-��x-1��2+4��
�ඥ��M���꣨1��4����
��A��3��0����C��0��3����M��1��4����
��2����ͼ2�У�����P��PN��y�ύAC��N����PQ=$\frac{\sqrt{2}}{2}$PN��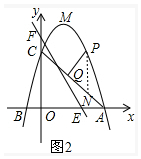
��P��a��-a2+2a+3����
��ֱ��AC����ʽΪy=-x+3��
��N��a��-a+3����
��PN=-a2+3a��0��a��3����
��a=-1��0��
�൱a=$\frac{3}{2}$ʱ��PN�����ֵ=$\frac{9}{4}$����ʱPQ�����ֵΪ$\frac{9\sqrt{2}}{8}$��
��3����ֱ��EF�Ľ���ʽΪy=-2x+4��
��E��2��0����F��0��4����$\frac{OF}{OE}$=2��
��ֱ��EF������һ�㣬������ÿ����1����λ�����������С2����λ��
����Լ���M�䣨1+m��4-2m����A�䣨3+m��-2m����C�䣨m��3-2m����
����A��C��2=18��A��P2=��$\frac{3}{2}$+m��2+��2m+$\frac{15}{4}$��2��C��P2=��m-$\frac{3}{2}$��2+��2m+$\frac{3}{4}$��2��
�ٵ���C��A��P=90��ʱ����A��C��2+A��P2=C��P2��
��18+��$\frac{3}{2}$+m��2+��2m+$\frac{15}{4}$��2=��m-$\frac{3}{2}$��2+��2m+$\frac{3}{4}$��2��
���m=-$\frac{7}{4}$��
��M��1��-$\frac{3}{4}$��$\frac{15}{2}$����
�ڵ���A��CP=90��ʱ����A��C��2+C��P2=A��P2��
��18+��m-$\frac{3}{2}$��2+��2m+$\frac{3}{4}$��2=��$\frac{3}{2}$+m��2+��2m+$\frac{15}{4}$��2��
���m=$\frac{1}{4}$��
��M��2��$\frac{5}{4}$��$\frac{7}{2}$����
�۵���A��PC��=90��ʱ����A��P2+PC��2=A��C��2��
�ࣨ$\frac{3}{2}$+m��2+��2m+$\frac{15}{4}$��2+��m-$\frac{3}{2}$��2+��2m+$\frac{3}{4}$��2=18��
���m=$\frac{-18��3\sqrt{31}}{20}$��
��M��3��$\frac{2+3\sqrt{31}}{20}$��$\frac{58-3\sqrt{31}}{10}$����M��4��$\frac{2-3\sqrt{31}}{20}$��$\frac{58+3\sqrt{31}}{10}$����
������������M�������ΪM��1��-$\frac{3}{4}$��$\frac{15}{2}$����M��2��$\frac{5}{4}$��$\frac{7}{2}$����M��3��$\frac{2+3\sqrt{31}}{20}$��$\frac{58-3\sqrt{31}}{10}$����M��4��$\frac{2-3\sqrt{31}}{20}$��$\frac{58+3\sqrt{31}}{10}$����
���� ���⿼����κ����ۺ��⡢һ�κ��������ɶ���������֮��ľ��빫ʽ��֪ʶ������Ĺؼ���ѧ�ṹ�����κ��������ֵ���⣬ѧ��������ۣ�ע�ⲻ��©�⣬�����п�ѹ���⣮


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
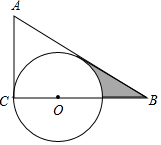 ��֪����ͼ����ABC�ġ�A=60�㣬��ACB=90�㣬BC=3����O��BC�ϣ���OC=1����OΪԲ�ģ�OC�İ뾶����O��
��֪����ͼ����ABC�ġ�A=60�㣬��ACB=90�㣬BC=3����O��BC�ϣ���OC=1����OΪԲ�ģ�OC�İ뾶����O���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -34 | B�� | -16 | C�� | 16 | D�� | 34 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com