
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 的对称轴是
的对称轴是![]() 轴,过点
轴,过点![]() 作一直线与抛物线
作一直线与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴的垂线与直线
轴的垂线与直线![]() 相交于点
相交于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)判断点![]() 是否在直线
是否在直线![]() 上,并说明理由;
上,并说明理由;
(3)若直线与抛物线有且只有一个公共点,且与抛物线的对称轴不平行,则称该直线与抛物线相切.过抛物线![]() 上的任意一点(除顶点外)作该抛物线的切线
上的任意一点(除顶点外)作该抛物线的切线![]() ,分别交直线
,分别交直线![]() 和直线
和直线![]() 于点
于点![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)在,见解析;(3)-8
;(2)在,见解析;(3)-8
【解析】
(1)由抛物线的对称轴是y轴可列式求出k,即可得到结果;
(2)过![]() 的直线与抛物线
的直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,设直线
两点,设直线![]() 的解析式为
的解析式为![]() 将
将![]() 代入
代入![]() ,得
,得![]() ,可判断出该方程有两个不相等的实数根
,可判断出该方程有两个不相等的实数根![]() ,
,![]() ,设
,设![]() ,
,![]() ,设出直线
,设出直线![]() 的解析式为
的解析式为![]() ,设
,设![]() ,
,![]() ,
,![]() ,计算可得
,计算可得![]() ,即可求出A的坐标,进行判断即可;
,即可求出A的坐标,进行判断即可;
(3)根据题意可设直线解析式![]() ,依题意得
,依题意得![]() ,得到
,得到![]() ,可求出切线
,可求出切线![]() 的解析式为
的解析式为![]() ,得到
,得到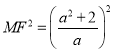 ,由勾股定理得
,由勾股定理得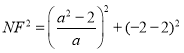 ,代入即可求解;
,代入即可求解;
解:(1)∵抛物线![]() 的对称轴是
的对称轴是![]() 轴,
轴,
∴![]() 且
且![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴抛物线![]() 的解析式为
的解析式为![]() .
.
(2)点![]() 在直线
在直线![]() 上.
上.
理由如下:∵过![]() 的直线与抛物线
的直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,
∴直线![]() 与
与![]() 轴不垂直.
轴不垂直.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() ,
,
∴该方程有两个不相等的实数根![]() ,
,![]() ,
,
不妨设![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
设![]() .
.
∵![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,
∴![]() ,
,
∴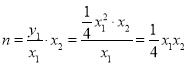 .
.
又方程![]() 的解为
的解为![]() ,
,
∴![]() ,
,
∴![]() ,
,
即点![]() 的纵坐标为-2,
的纵坐标为-2,
∴点![]() 在直线
在直线![]() 上.
上.
(3)∵切线![]() 不过抛物线
不过抛物线![]() 的顶点,
的顶点,
∴设切线![]() 的解析式为
的解析式为![]()
![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
依题意得![]() ,
,
即![]() ,
,
∴![]() ,
,
∴切线![]() 的解析式为
的解析式为![]() .
.
当![]() 时,
时,![]() ,∴
,∴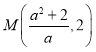 .·
.·
当![]() 时,
时,![]() ,∴
,∴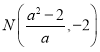 .
.
∵![]() ,
,
∴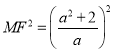 ,
,
由勾股定理得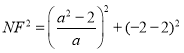 ,
,
∴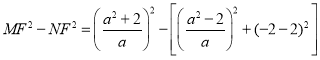
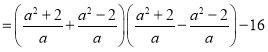
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与《新型冠状病毒防治与预防知识》作答(满分100分),社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩,并对他们的成绩(单位:分)进行数据统计、数据分析.
甲 | 85 | 80 | 95 | 85 | 90 | 95 | 100 | 65 | 75 | 85 |
90 | 90 | 70 | 100 | 90 | 80 | 80 | 90 | 98 | 75 | |
乙 | 80 | 60 | 80 | 85 | 95 | 65 | 90 | 85 | 100 | 80 |
95 | 75 | 80 | 80 | 70 | 100 | 95 | 75 | 90 | 90 |
表1分数统计表
成绩 小区 | 60≤x≤70 | 70<x≤80 | 80<x≤90 | 90<x≤100 |
甲 | 2 | 5 | a | b |
乙 | 3 | 7 | 5 | 5 |
表2:频数分布表
统计量 小区 | 平均数 | 中位数 | 众数 |
甲 | 85.75 | 87.5 | c |
乙 | 83.5 | d | 80 |
表3:统计量
(1)填空:a= ,b= ,c= ,d= ;
(2)甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;
(3)对于此次抽样调查中测试成绩为60≤x≤70的居民,社区鼓励他们重新学习,然后从中随机抽取两名居民进行测试,求刚好抽到一个是甲小区居民,另一个是乙小区居民的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 分别是射线
分别是射线![]() ,
,![]() 上的点.
上的点.
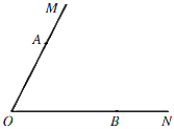
(1)尺规作图:在![]() 的内部确定一点
的内部确定一点![]() ,使得
,使得![]() 且
且![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)在(1)中,连接![]() ,用无刻度直尺在线段
,用无刻度直尺在线段![]() 上确定一点
上确定一点![]() ,使得
,使得![]() ,并证明
,并证明![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“新冠肺炎”肆虐时,无数抗疫英雄涌现,七年级(2)班老师为让同学们更深人地了解抗疫英雄钟南山、李兰娟、李文亮、张文宏(依次记为A、B、C、D)的事迹,设计了如下活动:取四张完全相同的卡片.分别写上A、B、C、D)四个标号,然后背面朝上放置在水平桌面上,搅匀后每个同学从中随机抽取一张卡片,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相对应抗疫英雄的资料,并做成小报.
(1)求小欢同学抽到的卡片上是钟南山的概率;
(2)请用列表法或画树状图的方法,求小平和小安两位同学抽到的卡片上是不同英雄的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生的安全意识情况,在全校范围内随机抽取部分学生进行问卷调查,根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下两幅尚不完整的统计图.

根据以上信息,解答下列问题:
(1)这次调查一共抽取了 名学生,其中安全意识为“很强”的学生占被调查学生总数的百分比是 ;
(2)请将条形统计图补充完整;
(3)该校有1800名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,估计全校需要强化安全教育的学生约有 名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在3×3正方形方格中,有3个小正方形涂成了黑色,所形成的图案如图所示,图中每块小正方形除颜色外完全相同.
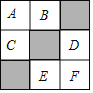
(1)一个小球在这个正方形方格上自由滚动,那么小球停在黑色小正方形的概率是多少?
(2)现将方格内空白的小正方形(A、B、C、D、E、F)中任取2个涂黑,得到新图案,请用列表或画树状图的方法求新图案是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的兴趣爱好,学校决定在七年级开设兴趣班,兴趣班设有四类:![]() 围棋班;
围棋班;![]() 象棋班;
象棋班;![]() 书法班;
书法班;![]() 摄影班.为了便于分班,年级组随机抽查了部分学生的选课意向(每人选报一类),并绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下问题:
摄影班.为了便于分班,年级组随机抽查了部分学生的选课意向(每人选报一类),并绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下问题:
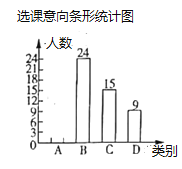
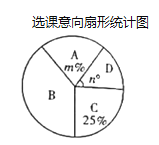
(1)求扇形统计图中![]() 、
、![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(2)已知该校七年级有600名学生,学校计划开设三个“围棋班”,每班要求不超过40人,实行随机分班.
①学校的开班计划是否能满足选择“围棋班”的学生意愿,说明理由;
②展鹏、展飞是一对双胞胎,他们都选择了“围棋班”,并且希望能分到同一个班,用树状图或列表法求他们的希望得以实现的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com