
分析 (1)根据“倍根方程”的定义,找出方程①、②中K的值,由此即可得出结论;
(2)将方程(x-2)(mx+n)=0整理成一般式,再根据“倍根方程”的定义,找出K=0,整理后即可得出4m2+5mn+n2的值;
(3)根据方程x2-$\sqrt{m}x+\frac{2}{3}$n=0(m≥0)是倍根方程即可得出m、n之间的关系,再由一次函数图象上点的坐标特征即可得出m、n之间的关系,进而即可求出m、n的值,此题得解.
解答 解:(1)在方程①x2-x-2=0中,K=(-1)2-$\frac{9}{2}$×1×(-2)=10≠1;
在方程②x2-6x+8=0中,K=(-6)2-$\frac{9}{2}$×1×8=0.
∴是倍根方程的是②x2-6x+8=0.
故答案为:②.
(2)整理(x-2)(mx+n)=0得:mx2+(n-2m)x-2n=0,
∵(x-2)(mx+n)=0是倍根方程,
∴K=(n-2m)2-$\frac{9}{2}$m•(-2n)=0,
∴4m2+5mn+n2=0.
(3)∵${x^2}-\sqrt{m}x+\frac{2}{3}n=0$是倍根方程,
∴$K={(-\sqrt{m})^2}-\frac{9}{2}×\frac{2}{3}n=0$,
整理得:m=3n.
∵A(m,n)在一次函数y=3x-8的图象上,
∴n=3m-8,
∴n=1,m=3,
∴此方程的表达式为${x^2}-\sqrt{3}x+\frac{2}{3}=0$.
点评 本题考查了根与系数的关系以及一次函数图象上点的坐标特征,熟练掌握“倍根方程”的定义是解题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
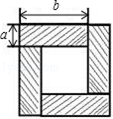 如图是用4个全等的长方形拼成的一个“回形”正方形,将图中阴影部分面积用2种方法表示可得一个等式,这个等式为(a+b)2-(b-a)2=4ab.
如图是用4个全等的长方形拼成的一个“回形”正方形,将图中阴影部分面积用2种方法表示可得一个等式,这个等式为(a+b)2-(b-a)2=4ab.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
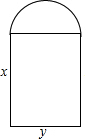 如图,一个门框的下部是长方形,上部是半圆形,已知长方形的长为x cm,宽为y cm,半圆的直径就是长方形的宽,怎样用x,y表示该门框的面积和周长?
如图,一个门框的下部是长方形,上部是半圆形,已知长方形的长为x cm,宽为y cm,半圆的直径就是长方形的宽,怎样用x,y表示该门框的面积和周长?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 收费(元) |
| 起步费3千米以下(含3千米) | 3 |
| 3千米以上,每增加1千米 | 1.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
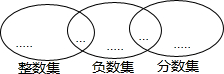 将下列各数填入相应集合圈中:
将下列各数填入相应集合圈中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com