练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．已知a2+b2-6a+4b+13=0，求[（2a+b）2-（2a-b）（a+b）-2（a-2b）（a+2b）]÷（$\frac{1}{3}$b）的值．

    分析 首先根据a2+b2-6a+4b+13=0，可得（a-3）2+（b+2）2=0，据此求出a、b的值各是多少；然后去括号，合并同类项，将代数式[（2a+b）2-（2a-b）（a+b）-2（a-2b）（a+2b）]÷（$\frac{1}{3}$b）化为最简式，再把a、b的值代入即可．

    解答 解：∵a2+b2-6a+4b+13=0，
    ∴（a-3）2+（b+2）2=0，
    ∴a-3=0，b+2=0，
    解得a=3，b=-2，
    ∴[（2a+b）2-（2a-b）（a+b）-2（a-2b）（a+2b）]÷（$\frac{1}{3}$b）
    =[4a2+4ab+b2-2a2-2ab+ab+b2-2a2+8b2]÷（$\frac{1}{3}$b）
    =[3ab+10b2]÷（$\frac{1}{3}$b）
    =9a+30b
    =9×3+30×（-2）
    =27-60
    =-33．

    点评 此题考查了配方法的应用，整式的混合运算-化简求值，要熟练掌握，解答此题的关键是要明确：给出整式中字母的值，求整式的值的问题，一般要先化简，再把给定字母的值代入计算，得出整式的值，不能把数值直接代入整式中计算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

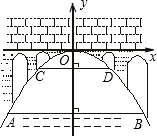    11．如图，有一座抛物线形拱桥，在正常水位时水面AB的宽为20m，如果水位上升15m，水面CD的宽是10m．
    （1）在如图所示的直角坐标系下，求此抛物线的解析式；
    （2）现有一辆载有救援物资的货车从甲地出发必须经过此桥开往乙地，已知甲地距此桥480km．货车正以每小时40km的速度开往乙地，当行驶1小时时，忽然接到紧急通知：前方连降暴雨，造成水位以每小时0.25m的速度持续上涨（货车接到通知时水位在CD处，当水位距桥拱最高点3m时，禁止车辆通行），试问：如果货车按原来速度行驶，能否安全通过此桥？若能，请说明理由；若不能，要使货车安全通过此桥，速度应超过每小时多少千米？
    （3）当货车接到紧急通知的同时，此桥上游40km处有一船只也接到该通知，此船正以每小时20km的最大速度顺水行驶而来，不知此船能否顺利通过此桥？请说明理由．（已知船的顶部距水面有3.5m高，船体上、下宽均为4m）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图，已知长方形的长为a，宽为2，两个半圆的直径都为2，用含a的式子表示出阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．读一读：式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和．由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“1+2+3+4+5+…+100”表示为$\sum_{n=1}^{100}$n，这里“$\sum{\;}$”是求和符号．例如：1+3+5+7+9+…+99，即从1开始的100以内的连续奇数的和，可表示为$\sum_{n=1}^{50}{\;}$（2n-1）；又如13+23+33+43+53+63+73+83+93+103可表示为$\sum_{n=1}^{10}{\;}$n3．    通过对上以材料的阅读，请解答下列问题．
    （1）2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符合可表示为$\sum_{n=1}^{50}2n$；
    （2）计算$\sum_{n=2}^{40}$（$\frac{1}{2}$n-1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

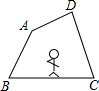    8．如图，小明沿画在地面上的四边形ABCD的边逆时针走一圈回到原地．
    （1）小明一共旋转的度数是360°；
    （2）请在图中标出小明在每个顶点处转过的角度；
    （3）小明所转过的角度的总和可以用式子表示为4×180°-（4-2）•180°；
    （4）如果顺时针走一圈呢？如果小明沿五边形、六边形、n边形的边走一圈呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知一元二次不等式ax2+bx+6＞0的解集为-2＜x＜3，求a，b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．观察下列等式：
    ①$\frac{1}{1×2}$=1-$\frac{1}{2}$，②$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，③$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$．
    将以上三个等式两边分别相加，得
    $\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
    （1）请写出第④个式子$\frac{1}{4×5}$=$\frac{1}{4}-\frac{1}{5}$
    （2）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$．
    （3）探究并计算：$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{100×102}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

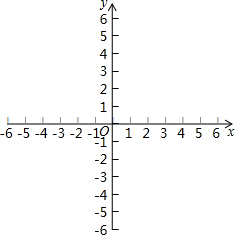    2．画出函数y=2x+4的图象，利用图象：
    （1）求方程2x+4=0的解：
    （2）求不等式2x+4＞0的解集：
    （3）若-2≤y≤5，求x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知直线l与直线l外一点P，求作：过点P且垂直于直线l的垂线a（尺规作图）．
    现给出一种作法，如下：
    步骤一：在直线l外取一点E，以点P为圆心，以线段PE为半径画弧，交直线l于点M，N；
    步骤二：分别以点M、N为圆心，大于$\frac{1}{2}$线段MN为半径画弧，过两弧的交点的直线a就是所求作的垂线．
    （1）按上述操作步骤，请成功作出过点P且垂直于直线l的垂线a．（符合要求的一种图形），并说明理由．
    （2）从你作图的过程中，思考要保证这种作法顺利作出，线段PE应该满足什么条件？
    （3）为了避免这种情况产生，小明说只要在直线l上取点E好了，并给出了画法，画法对吗？请说明理由．
    （作法：在直线l上取两点B、D，以P为圆心，以PD 为半径画圆交直线l于点E，以P为圆心，以PB 为半径画圆交直线l于点F，其中较小圆分别交PB，PF于点M、N，连接E、N和D、M，EN和MD相交于点H，则PH就是所求的垂线．）
    （4）请在直线l上取点E，用直尺和圆规过点P且垂直于直线l的垂线a（与小明不同的方法，并要求尽可能简单）．

    查看答案和解析>>

    同步练习册答案