
【题目】如图,![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】淇淇和嘉嘉在学习了利用相似三角形测高之后分别测量两个旗杆高度.
(1)如图1所示,淇淇将镜子放在地面上,然后后退直到她站直身子刚好能从镜子里看到旗杆的顶端E,测得脚掌中心位置B到镜面中心C的距离是50cm,镜面中心C距离旗杆底部D的距离为4m,已知淇淇同学的身高是1.54m,眼睛位置A距离淇淇头顶的距离是4cm,求旗杆DE 的高度.

如图2所示,嘉嘉在某一时刻测得 1 米长的竹竿竖直放置时影长2米,在同时刻测量旗杆的影长时,旗杆的影子一部分落在地面上(BC),另一部分落在斜坡上(CD),他测得落在地面上的影长为10米,落在斜坡上的影长为![]() 米,∠DCE=45°,求旗杆AB的高度?
米,∠DCE=45°,求旗杆AB的高度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是
与x轴交于A、B(A在B左侧)两点, 一次函数y=-x+4与坐标轴分别交于点C、D,与抛物线交于点M、N,其中点M的横坐标是![]() .
.
(1)求出点C、D的坐标;
(2)求抛物线的表达式以及点A、B的坐标;
(3)在平面内存在动点P(P不与A,B重合),满足∠APB为直角,动点P到直线CD的距离是否有最小值,如果有,请直接写出这个最小值的结果;如果没有,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
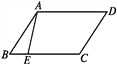
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]()
(1)如图1,若![]() ,则
,则![]() (直接写出结果) .
(直接写出结果) .
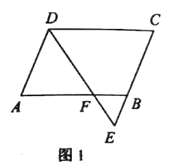
(2)如图2,若![]() 为
为![]() 的点,连接
的点,连接![]() ,求
,求![]() 的值;
的值;
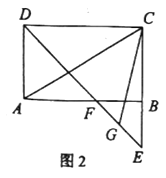
(3)如图3,若![]() 连接
连接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com