
 如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:
如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接BF、DE交于点O,连接EF,给出如下结论:分析 ①根据直角三角形的面积公式易得S△BEF=S△DEF,易推知①正确;
②连接BD,由BF、DE分别是△ABD的两条中线易得②正确;
③当EF=2时,设AE=x,AF=y,则由勾股定理得到:x2+y2=4,然后由x、y分别表示出BF、DE,不难得到BF2+DE2=20,即③不成立;
④EF=2时,设AE=x,AF=y,则x2+y2=4,结合矩形的面积得到:4xy=10,易求矩形ABCD的周长为12.
解答  解:连接BD,由BF、DE分别是△ABD的两条中线易得S△BEF=S△DEF即S△BEO=S△DFO、
解:连接BD,由BF、DE分别是△ABD的两条中线易得S△BEF=S△DEF即S△BEO=S△DFO、
S四边形AEOF=$\frac{1}{6}$S矩形ABCD成立,
故①②正确;
当EF=2时,设AE=x,AF=y,则x2+y2=4,
又S矩形ABCD=10,即4xy=10,
∴xy=2.5,x+y=3,
∴矩形ABCD周长为12,
故④正确;
当EF=2时,设AE=x,AF=y,则x2+y2=4,
BF2=(2x)2+y2,DE2=x2+(2y)2,
∴BF2+DE2=5x2+5y2=5(x2+y2),即BF2+DE2=20,即③不成立,
故③错误.
综上所述,①②④成立.
故答案是:①②④.
点评 本题考查了四边形综合题,需要掌握矩形的性质、勾股定理、矩形面积的求法、矩形周长的求法以及三角形面积的计算,属于难题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
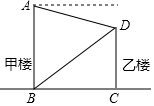 如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示)
如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.
如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是用完全相同的火柴棍拼成一排由三角形组成的图形示意图.若拼成的图形中有n个菱形,则需要火柴棍的根数是( )
如图是用完全相同的火柴棍拼成一排由三角形组成的图形示意图.若拼成的图形中有n个菱形,则需要火柴棍的根数是( )| A. | n+4 | B. | 2n+1 | C. | 2n+3 | D. | 4n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
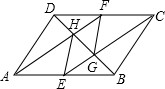 如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.
如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,在四边形ABCD中,∠B=∠C,点E,F,G分别在AB,BC,CD上,且AE=GF=GC.
已知:如图所示,在四边形ABCD中,∠B=∠C,点E,F,G分别在AB,BC,CD上,且AE=GF=GC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com