
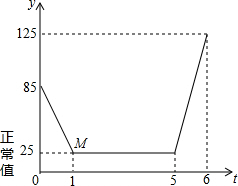
 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.小强家PM2.5的浓度随着时间变化的图象如图所示,请根据图象解答下列问题:分析 (1)点M表示的实际意义为:当使用空气净化器1小时时,PM2.5浓度恰好降低至25mg/m3的正常值.
(2)设第一小时内,y-5t的函数表达式为y=kt+b(k≠0),图象经过(0,85)(1,25)代入得:$\left\{\begin{array}{l}b=85\\ kt+b=25\end{array}\right.$,解方程组即可;
(3)结合实际问题的解析意义可知,$\frac{60}{1}$=$\frac{125-25}{t}$,解得t=$\frac{5}{3}$,由此即可解决问题;
解答 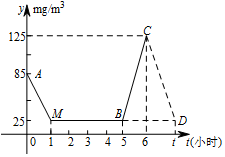 解:(1)点M表示的实际意义为:当使用空气净化器1小时时,PM2.5浓度恰好降低至25mg/m3的正常值.
解:(1)点M表示的实际意义为:当使用空气净化器1小时时,PM2.5浓度恰好降低至25mg/m3的正常值.
(2)解:设第一小时内,y-5t的函数表达式为y=kt+b(k≠0),
∵图象经过(0,85)(1,25)代入得:$\left\{\begin{array}{l}b=85\\ kt+b=25\end{array}\right.$
解得:$\left\{\begin{array}{l}k=-60\\ b=85\end{array}\right.$,
∴函数表达式为y=-60t+85(0≤t≤1)
(3)解:结合实际问题的解析意义可知,$\frac{60}{1}$=$\frac{125-25}{t}$,
解得t=$\frac{5}{3}$,
∴预计经过$\frac{5}{3}$小时,PM2.5浓度恢复正常.
点评 本题考查一次函数的应用、待定系数法等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会利用图中信息解决问题,属于中考常考题型.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:解答题
 用直尺和圆规作图(不写作法,只保留作图痕迹):
用直尺和圆规作图(不写作法,只保留作图痕迹):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
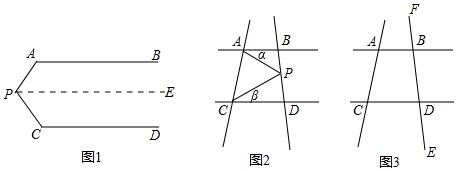
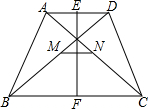 已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.
已知:如图,在四边形ABCD中,AD∥BC,AB=DC,E、F、M、N分别是AD、BC、BD、AC的中点,试说明:EF与MN互相垂直平分.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
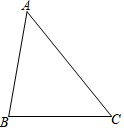
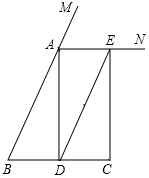 已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD是△ABC的中线,AN为△ABC的外角∠CAM的平分线,CE∥AD,交AN于点E.求证:四边形ADCE是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
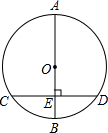 如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )
如图,⊙O的直径AB=20cm,CD是⊙O的弦,AB⊥CD,垂足为E,OE:EB=3:2,则CD的长是( )| A. | 10cm | B. | 14cm | C. | 15cm | D. | 16cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000 | B. | 1000名 | ||
| C. | 43735名考生的数学成绩 | D. | 1000名考生的数学成绩 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com