
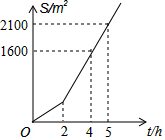
 某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 500 | B. | 400 | C. | 300 | D. | 200 |
分析 根据待定系数法可求直线AB的解析式,再根据函数上点的坐标特征得出当x=2时,y的值,再根据工作效率=工作总量÷工作时间,列出算式求出该绿化组提高工作效率前每小时完成的绿化面积.
解答 解:如图,设直线AB的解析式为y=kx+b,则
$\left\{\begin{array}{l}{4k+b=1600}\\{5k+b=2100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=500}\\{b=-400}\end{array}\right.$.
故直线AB的解析式为y=500x-400,
当x=2时,y=500×2-400=600,
600÷2=300(m2).
答:该绿化组提高工作效率前每小时完成的绿化面积是300m2.
故选:C.
点评 考查了一次函数的应用和函数的图象,关键是根据待定系数法求出该绿化组提高工作效率后的函数解析式,同时考查了工作效率=工作总量÷工作时间的知识点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a>3b | B. | a-3>b-3 | C. | -3a>-3b | D. | $\frac{a}{3}$>$\frac{b}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
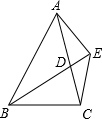 如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.
如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com