
【题目】如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.

【答案】(1)证明见解析;(2)平行四边形ABCD的面积= 4![]() .
.
【解析】试题分析:(1)根据平行四边形的性质得到AB∥CD,AB=CD,然后根据CE=DC,得到AB=EC,AB∥EC,利用“一组对边平行且相等的四边形是平行四边形”判断即可;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得出四边形ABEC是矩形,得出∠BAC=90°,由勾股定理求出AC,即可得出平行四边形ABCD的面积.
试题解析:
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,BC=AD,
∵CE=DC,∴AB=EC,AB∥EC,∴四边形ABEC是平行四边形,∴BF=CF;
(2)解:∵由(1)知,四边形ABEC是平行四边形,∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,∴∠ABC=∠D.又∵∠AFC=2∠D,∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,∴∠ABC=∠BAF,∴FA=FB,∴FA=FE=FB=FC,∴AE=BC,
∴四边形ABEC是矩形,∴∠BAC=90°,
∵BC=AD=4,∴AC=![]() =
=![]() =2
=2![]() ,
,
∴平行四边形ABCD的面积=ABAC=2×2![]() =4
=4![]() .
.


科目:初中数学 来源: 题型:
【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计I绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
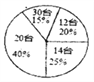
A. 19,20,14 B. 18.4,20,20 C. 19, 20, 20 D. 18.4,25,20
查看答案和解析>>
科目:初中数学 来源: 题型:
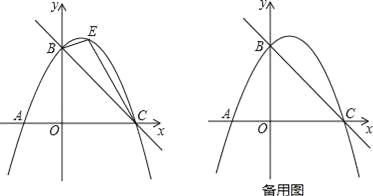
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
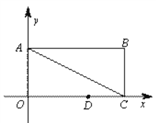
【题目】如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.
(1)求直线AC的解析式.
(2)在y轴上是否存在点P,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)抛物线y=-x2经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且△ODE沿DE折叠后点O落在边AB上O/处?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在九年级学生中开展以“每天数学家庭作业完成时间”设置的一个问题,有以下选项:
A.0~0.5小时B.0.5~1个小时 C.1个小时~1.5个小时 D.1.5个小时以上
在随机调查了九(1)班学生后,根据相关数据给出如图所示的统计图.
(1)该校九(1)班学生 人;做数学家庭作业1.5个小时以上的占 ;
(2)补全频数直方图;
(3)已知该校九年级共400名学生,据此推算,该校九年级学生中,“做数学家庭作业1.5个小时以上”的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
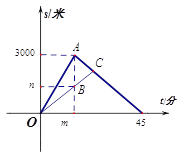
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸距出发地1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
(1)图中![]() ,
, ![]() ;
;
(2)求小明和爸爸相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的表示如图所示,则下列结论中: ①ab<0, ②![]() <0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
<0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com