
【题目】火车站、机场、邮局等场所都有为旅客提供打包服务的项目.现有一个长、宽、高分别为a、b 、30的箱子(其中a>b),准备采用如图①、②的两种打包方式,所用打包带的总长(不计接头处的长)分别记为![]() .
.

(1)图①中打包带的总长![]() =________.
=________.
图②中打包带的总长![]() =________.
=________.
(2)试判断哪一种打包方式更节省材料,并说明理由.(提醒:先判断再说理,说理过程即为比较 ![]() 的大小.)
的大小.)
(3)若b=40且a为正整数,在数轴上表示数![]() 的两点之间有且只有19个整数点,求a 的值.
的两点之间有且只有19个整数点,求a 的值.
【答案】(1)l=4a+2b+180,l=2a+4b+180;(2)第2种,l- l=2(a-b),理由见解析;
(3)a=50
【解析】
(1)根据图形,不难看出:图①打包带的长有长方体的四个长、两个宽、六个高,图②打包带的长有长方体的两个长、四个宽、六个高,从而可以解答本题;
(2)根据(1)中的答案可以求得哪一种打包方式更节省材料;
(3)根据(2)中的关系式,代入b的值,再根据![]() 的两点之间有且只有19个整数点即可求解.
的两点之间有且只有19个整数点即可求解.
解:(1)图①四个长为4a,两个宽为2b,六个高为30×6=180,
∴打包带的长l=4a+2b+180,
图②两个长为2a,四个宽为4b,六个高为30×6=180,
∴打包带的长l=2a+4b+180,
故答案为l=4a+2b+180,l=2a+4b+180.
(2)第2种打包方式更节省材料,理由如下:
(4a+2b+180)-(2a+4b+180),
=4a+2b+180-2a-4b-180,
=2(a-b),
∵![]() ,
,
∴2(a-b)>0,
∴第2种打包方式更节省材料;
(3)当![]() 时, 2(a-b)=2(a-40) =2a-80,
时, 2(a-b)=2(a-40) =2a-80,
∵在数轴上表示数![]() 的两点之间有且只有19个整数点, 且
的两点之间有且只有19个整数点, 且![]() 为正整数,
为正整数,
∴a=50.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 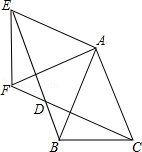
(1)求证:BE=CF;
(2)当四边形ACDE为菱形时,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△P1OA1 , △P2A1A2都是等腰直角三角形,点P1 , P2都在函数y= ![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( ) 
A.(4 ![]() ,
, ![]() )
)
B.(4+2 ![]() ,4﹣2
,4﹣2 ![]() )??
)??
C.(2+2 ![]() ,2
,2 ![]() ﹣2)
﹣2)
D.(4+2 ![]() ,2+2
,2+2 ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 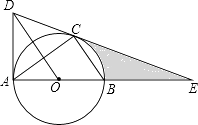
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=6,CE=2 ![]() . ①求⊙O的半径
. ①求⊙O的半径
②求线段CE,BE与劣弧 ![]() 所围成的图形的面积(结果保留根号和π)
所围成的图形的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2+bx+3交y轴于点A,交x轴正半轴于点C(3,0),交x轴负半轴于点B(﹣1,0),∠ACB=45°.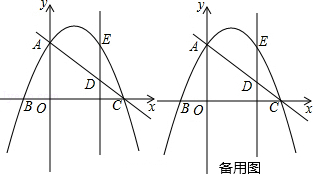
(1)求此抛物线的解析式;
(2)点D为线段AC上一点,且AD=2CD,过点D作DE∥y轴,交抛物线一点E,点P为x轴上方抛物线的一点,设点P的横坐标为t,△PDE的面积为s,求s与t之间的函数关系式,并直接写出t的范围;
(3)在(2)的条件下,过点P作PF∥DE交直线AC于点F,是否存在点P,使以点P、F、E、D为顶点的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
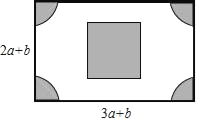
【题目】如图,有一块长(3a+b)米,宽(2a+b)米的长方形广场,园林部门要对阴影区域进行绿化,空白区域进行广场硬化,其中,四个角部分是半径为(a﹣b)米的四个大小相同的扇形,中间部分是边长为(a+b)米的正方形.
(1)用含a、b的式子表示需要硬化部分的面积;
(2)若a=30,b=10,求出硬化部分的面积(结果保留π的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
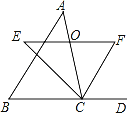
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E,F.
(1)若CE=4,CF=3,求OC的长.
(2)连接AE、AF,问当点O在边AC上运动到什么位置时,四边形AECF是矩形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习一元一次方程的解法时,我们经常遇到这样的试题:
“解方程:![]() ”,请根据解题过程,在后面的括号内写出变形依据.
”,请根据解题过程,在后面的括号内写出变形依据.
解:去分母,得 ( )
去括号,得 ( )
移项,得 ( )
合并,得 (合并同类项法则)
系数化为 1,得 ( )
请你写出在进行运算时容易出错的地方(至少写出三个).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com