
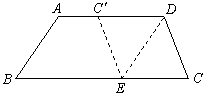
如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形CDC′E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
 |
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合 ,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
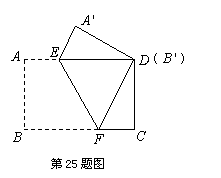
把一张矩形纸片ABCD按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB = 3 cm,BC =4 cm.
(1)求线段DF的长;
(2)连接BE,求证:四边形BFDE是菱形;
(3)求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
【感知】如图①,当点H与点C重合时,可得FG=FD.
【探究】如图②,当点H为边CD上任意一点时, 猜想FG与FD的数量关系,并说明理由.
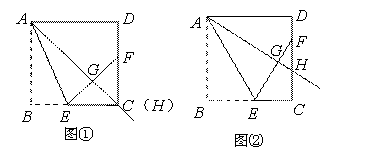 【应用】在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.
【应用】在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com