
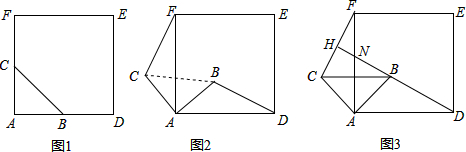
分析 (1)根据旋转变换的性质和全等三角形的判定定理证明△CAF≌△BAD,证明结论;
(2)①根据全等三角形的性质、垂直的定义证明即可;
②作BM⊥AD于M,在Rt△AMB中,由∠BAM=45°,AB=2,推出AM=BM=$\sqrt{2}$,DM=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,由BM∥AN,推出$\frac{BM}{AN}$=$\frac{DM}{DA}$即可解决问题;
解答 解:(1)BD=CF.
理由如下:如图2中,由题意得,∠CAF=∠BAD=θ,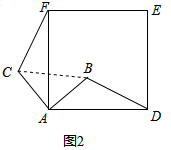
在△CAF和△BAD中,
$\left\{\begin{array}{l}{CA=BA}\\{∠CAF=∠BAD}\\{FA=DA}\end{array}\right.$,
∴△CAF≌△BAD,
∴BD=CF;
(2)①由(1)得△CAF≌△BAD,
∴∠CFA=∠BDA,
∵∠FNH=∠DNA,∠DNA+∠NDA=90°,
∴∠CFA+∠FNH=90°,
∴∠FHN=90°,即BD⊥CF;
②如图3中,作BM⊥AD于M,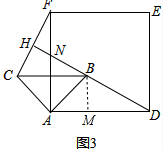
在Rt△AMB中,∵∠BAM=45°,AB=2,
∴AM=BM=$\sqrt{2}$,DM=3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$,
BM∥AN,
∴$\frac{BM}{AN}$=$\frac{DM}{DA}$,
∴$\frac{\sqrt{2}}{AN}$=$\frac{2\sqrt{2}}{3\sqrt{2}}$,
∴AN=$\frac{3\sqrt{2}}{2}$
点评 本题考查的是正方形的性质、等腰直角三角形的性质、旋转变换的性质以及相似三角形的判定和性质,掌握旋转角的定义和旋转变换的性质、正确作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
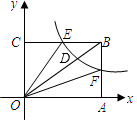 如图,在矩形OABC中,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.
如图,在矩形OABC中,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$的图象与BC边交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
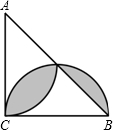 如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )
如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )| A. | $\frac{π}{4}$-$\frac{1}{2}$ | B. | $\frac{3π}{4}$-$\frac{3}{2}$ | C. | $\frac{3π}{4}$-$\frac{3}{4}$ | D. | $\frac{π}{4}$+$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
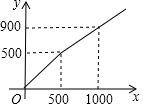 某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是( )
某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是( )| A. | 打六折 | B. | 打七折 | C. | 打八折 | D. | 打九折 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2)m | B. | ($\frac{1}{2}$)m | C. | m-2 | D. | m${\;}^{\frac{1}{2}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线AB:y1=x+m与双曲线C;y2=$\frac{k}{x}$相交于A、B两点,其中A点(2,5),AC⊥y轴于C.
如图,在平面直角坐标系中,直线AB:y1=x+m与双曲线C;y2=$\frac{k}{x}$相交于A、B两点,其中A点(2,5),AC⊥y轴于C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com