
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
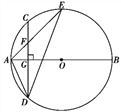
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】分析:①利用垂径定理可知![]() ,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且
,可知∠ADF=∠AED,结合公共角可证明△ADF∽△AED;②结合CF=2,且![]() ,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=
,可求得DF=6,且CG=DG,可求得FG=2;③在Rt△AGF中可求得AG,在Rt△AGD中可求得tanADG=![]() ,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7
,且∠E=∠ADG,可判断出③;④可先求得S△ADF,再求得△ADF∽△AED的相似比,可求出S△ADE=7![]() .
.
详解:①∵AB为直径,AB⊥CD,
∴![]() ,
,
∴∠ADF=∠AED,且∠FAD=∠DAE,
∴△ADF∽△AED,
∴①正确;
②∵AB为直径,AB⊥CD,
∴CG=DG,
∵![]() ,且CF=2,
,且CF=2,
∴FD=6,
∴CD=8,
∴CG=4,
∴FG=CG-CF=4-2=2,
∴②错误;
③在Rt△AGF中,AF=3,FG=2,
∴AG=![]() ,且DG=4,
,且DG=4,
∴tan∠ADG=![]() ,
,
∵∠E=∠ADG,
∴tan∠E=![]() ,
,
∴③错误;
④在Rt△ADG中,AG=![]() ,DG=4,
,DG=4,
∴AD=![]() ,
,
∴![]() ,
,
∴△ADF∽△AED中的相似比为![]() ,
,
∴![]() ,
,
在△ADF中,DF=6,AG=![]() ,
,
∴S△ADF=![]() DFAG=
DFAG=![]() ×6×
×6×![]() =3
=3![]() ,
,
∴![]() ,
,
∴S△ADE=7![]() ,
,
∴④错误;
∴正确的有①一个.
故选:A.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】直线![]() 与
与![]() 轴、
轴、![]() 轴分別交于
轴分別交于![]() 、
、![]() 两点,
两点,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上一点.
上一点.
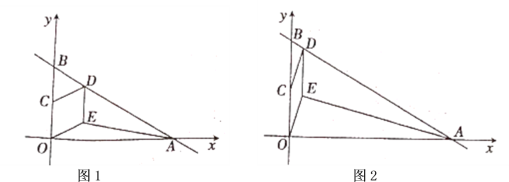
(1)求点![]() 、
、![]() 的坐标;
的坐标;
(2)若四边形![]() 是菱形,如图1,求
是菱形,如图1,求![]() 的面积;
的面积;
(3)若四边形![]() 是平行四边形,如图2,设点
是平行四边形,如图2,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 上的一动点(不与点
上的一动点(不与点![]() 重合),延长
重合),延长![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 填空:①当
填空:①当![]() ________时,四边形
________时,四边形![]() 是矩形;②当
是矩形;②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=![]() .
.
(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:![]() +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:
“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.
问题解决:(填出依据)
解:(1)如图①,延长AB到E,过点B作BF∥AC.
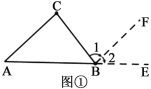
∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
(2)类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°”
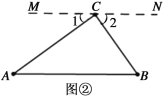
(3)拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E= .
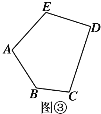
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>9且x<26,单位:km)
第一次 | 第二次 | 第三次 | 第四次 |
x |
| x﹣5 | 2(9﹣x) |
(1)说出这辆出租车每次行驶的方向.
(2)求经过连续4次行驶后,这辆出租车所在的位置.
(3)这辆出租车一共行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a、b、c在数轴上的位置如图所示
![]()
(1)比较a、b、|c|的大小(用“>”连接);
(2)若n=|b+c|﹣|c﹣1|﹣|b﹣a|,求![]() 的值;
的值;
(3)若a=![]() ,b=﹣2,c=﹣3,且a、b、c对应的点分别为A、B、C,问在数轴上是否存在一点M,使M与B的距离是M与A的距离的3倍,若存在,请求出M点对应的有理数;若不存在,请说明理由.
,b=﹣2,c=﹣3,且a、b、c对应的点分别为A、B、C,问在数轴上是否存在一点M,使M与B的距离是M与A的距离的3倍,若存在,请求出M点对应的有理数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com