
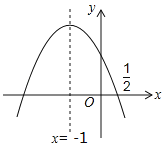
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
【答案】①③⑤.
【解析】试题由抛物线的开口向下可得:a<0,根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,根据抛物线与y轴的交点在正半轴可得:c>0,∴abc>0,故①正确;
直线![]() 抛物线
抛物线![]() 的对称轴,所以
的对称轴,所以![]() ,可得b=2a,a﹣2b+4c=a﹣4a+2=﹣3a+4c,∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;
,可得b=2a,a﹣2b+4c=a﹣4a+2=﹣3a+4c,∵a<0,∴﹣3a>0,∴﹣3a+4c>0,即a﹣2b+4c>0,故②错误;
∵抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),∴抛物线与x轴的另一个交点坐标为(
,0),∴抛物线与x轴的另一个交点坐标为(![]() ,0),当x=
,0),当x=![]() 时,y=0,即
时,y=0,即![]() ,整理得:25a﹣10b+4c=0,故③正确;
,整理得:25a﹣10b+4c=0,故③正确;
∵b=2a,a+b+c<0,∴![]() ,即3b+2c<0,故④错误;
,即3b+2c<0,故④错误;
∵x=﹣1时,函数值最大,∴![]() (m≠1),∴a﹣b>m(am﹣b),所以⑤正确;
(m≠1),∴a﹣b>m(am﹣b),所以⑤正确;
故答案为:①③⑤.


科目:初中数学 来源: 题型:
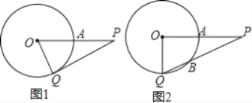
【题目】已知P是⊙O外的一点,OP=4,OP交⊙O于点A,且A是OP的中点,Q是⊙O上任意一点.
(1)如图1,若PQ是⊙O的切线,求∠QOP的大小;
(2)如图2,若∠QOP=90°,求PQ被⊙O截得的弦QB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
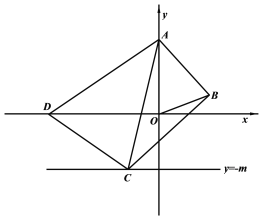
【题目】已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线![]() 于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
(1)求证:△ABC≌△AOD.
(2)设△ACD的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(3)若四边形ABCD恰有一组对边平行,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
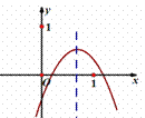
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列代数式:①ac;②a+b+c;③4a-2b+c;④2a+b;⑤b2-4ac中,值大于0的序号为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学有库存1800套旧桌凳,修理后捐助贫困山区学校.现有甲,乙两个木工组都想承揽这项业务.经协商后得知:甲木工组每天修理的桌凳套数是乙木工组每天修理桌凳套数的![]() ,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
,甲木工组单独修理这批桌凳的天数比乙木工组单独修理这批桌凳的天数多10天,甲木工组每天的修理费用是600元,乙木工组每天的修理费用是800元.
(1)求甲,乙两木工组单独修理这批桌凳的天数;
(2)现有三种修理方案供选择:方案一,由甲木工组单独修理这批桌凳;方案二,由乙木工组单独修理这批桌凳;方案三,由甲,乙两个木工组共同合作修理这批桌凳.请计算说明哪种方案学校付的修理费最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过A(1,1)和B(2,﹣1)
(1)求一次函数y=kx+b的表达式;
(2)求直线y=kx+b与坐标轴围成的三角形的面积;
(3)将一次函数y=kx+b的图象沿y轴向下平移3个单位,则平移后的函数表达式为 ,再向右平移1个单位,则平移后的函数表达式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
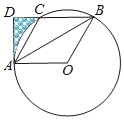
【题目】如图,⊙O的半径为6,点A,B,C为⊙O上三点,BA平分∠OBC,过点A作AD⊥BC交BC延长线于点D.
(1)求证:AD是⊙O的切线;
(2)当sin∠OBC=![]() 时,求BC的长;
时,求BC的长;
(3)连结AC,当AC∥OB时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
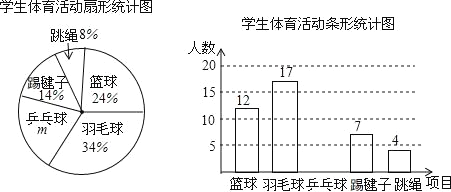
(1)m= %,这次共抽取了 名学生进行调查;并补全条形图;
(2)请你估计该校约有 名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用列表或画树状图的方法,求抽到一男一女学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
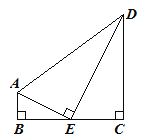
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com