
 如图,等腰△ABC中,AB=AC,ED是AB边中垂线,若BD=BC,则∠1的度数是54°.
如图,等腰△ABC中,AB=AC,ED是AB边中垂线,若BD=BC,则∠1的度数是54°. 分析 根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BDC=2∠A,根据等边对等角可得∠C=∠BDC,∠C=∠ABC,然后利用三角形的内角和等于180°求出∠A的度数,再根据直角三角形两锐角互余求出∠2,然后根据对顶角相等解答即可.
解答  解:∵ED是AB边中垂线,
解:∵ED是AB边中垂线,
∴AD=BD,
∴∠A=∠ABD,
在△ABD中,∠BDC=∠A+∠ABD=2∠A,
∵BD=BC,AB=AC,
∴∠C=∠BDC,∠C=∠ABC,
在△ABC中,∠A+∠ABC+∠C=∠A+2∠A+2∠A=180°,
解得∠A=36°,
∵DE⊥AB,
∴∠2=90°-∠A=90°-36°=54°,
∴∠1=∠2=54°.
故答案为:54°.
点评 本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等角对等边的性质,三角形内角和定理,对顶角相等的性质,把∠ABC、∠C都用∠A表示出来是解题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$=( )
如图,在平行四边形ABCD中,点E是边AD上一点,且AE=2ED,EC交对角线BD于点F,则$\frac{EF}{FC}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k1=1,k2=-2 | B. | k1=1,k2=2 | C. | k1=-1,k2=-2 | D. | k1=1,k2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.
如图,四边形OABC是矩形,四边形ADEF是正方形,点A,D在x轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B,E在反比例函数y=$\frac{k}{x}$的图象上,OA=2,OC=12,则正方形ADEF的边长为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-3$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{\frac{2}{3}}$×$\sqrt{6}$=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
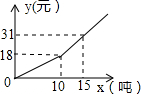 我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元.
我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水18吨,则应交水费38.8元.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com