
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

【答案】(1)此时小强头部E点与地面DK相距约为144.5cm(2)他应向前9.5cm
【解析】试题分析:(1)过点F作FN⊥DK于N,过点E作EM⊥FN于M,利用三角函数求出FM,FN的值即可解决问题,(2)过点E作EP⊥AB于点P,延长OB交MN于N,分别求出OH,PH的值即可做出判断.
(1)如图,过点F作FN⊥DK于N,过点E作EM⊥FN于M.∵EF+FG=166cm,FG=100cm,∴EF=66cm.∵∠FGK=80°,∴FN=100·sin80°≈98cm.
∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°,∴FM=66·cos45°≈46.53cm,∴MN=FN+FM≈144.5cm.∴此时小强头部E点与地面DK相距约为144.5cm.
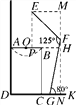
(2)如图,过点E作EP⊥AB于点P,延长OB交MN于H.∵AB=48cm,O为AB中点,∴AO=BO=24cm.∵EM=66·sin45°≈46.53(cm),∴PH≈46.53(cm).
∵GN=100·cos80°≈17(cm),CG=15cm,∴OH=24+15+17=56(cm),OP=OH-PH=56-46.53=9.47≈9.5cm,∴他应向前9.5cm


科目:初中数学 来源: 题型:
【题目】在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
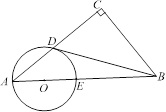
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】望江中学为了了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计,并将调查统计的结果分为:每天诵读时间t≤20分钟的学生记为A类,20分钟<t≤40分钟的学生记为B类,40分钟<t≤60分钟的学生记为C类,t>60分钟的学生记为D类四种.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
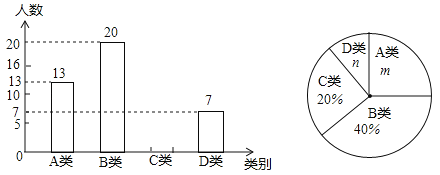
(1)m=%,n=%,这次共抽查了名学生进行调查统计;
(2)请补全上面的条形统计图;
(3)如果该校共有1200名学生,请你估计该校C类学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,假命题的是( )
A. 四个角都相等的四边形是矩形
B. 两组对边分别相等的四边形是平行四边形
C. 对角线互相垂直且相等的四边形是正方形
D. 两条对角线互相垂直平分的四边形是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
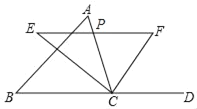
【题目】如图,△ABC中,点P是AC边上一个动点,过P作直线EF∥BC,交∠ACB的平分线于点E,交∠ACB的外角∠ACD平分线于点F.
(1)请说明:PE=PF;
(2)当点P在AC边上运动到何处时,四边形AECF是矩形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复上述过程,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.64 | 0.58 | 0.605 | 0.601 |
(1)请将表中的数据补充完整,
(2)请估计:当n很大时,摸到白球的概率约是 .(精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=DC,E,F,G,H分别是AD,BC,BD,AC的中点.
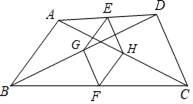
(1)证明:EG=EH;(2)证明:四边形EHFG是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承中华优秀的传统文化,市教育局决定开展“经典诵读进校园”活动,某校园团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表:
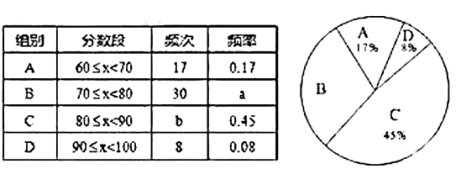
请根据所给信息,解答以下问题:
(1)表中![]() ;
;![]() ;
;
(2)请计算扇形统计图中![]() 组对应的圆心角的度数;
组对应的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列举法或树状图法求甲、乙两名同学都被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第一象限,斜靠在两条坐标轴上,且点A(0,2),点C(1,0),BE⊥x轴于点E,一次函数y=x+b经过点B,交y轴于点D.
(1)求证:△AOC≌△CEB;
(2)求△ABD的面积.
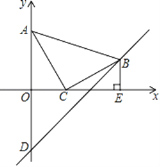
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com