
【题目】如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30方向12km处,位于景点B的正北方向,还位于景点C的北偏西75方向上.已知AB=![]() km.
km.
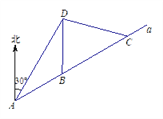
(1)现准备由景点D向公路a修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;
(2)求出景点B与景点C之间的距离(结果保留根号).
【答案】(1)6km;(2)![]() .
.
【解析】试题分析:(1) 过点D作DE⊥AC于点E,过点A作AF⊥DB,交DB的延长线于点F,求DE的问题就可以转化为求∠DBE的度数或三角函数值的问题;(2)Rt△DCE中根据三角函数就可以求出CD的长.
试题解析: (1)如图,过点D作DE⊥AC于点E,

过点A作AF⊥DB,交DB的延长线于点F,
在Rt△DAF中,∠ADF=30°,
∴AF=![]() AD=
AD=![]() ×12=6,
×12=6,
∴DF=![]() =
=![]() =6
=6![]() ,
,
在Rt△ABF中BF=![]() =
=![]() =2
=2![]() ,
,
∴BD=DFBF=6![]() -2
-2![]() =4
=4![]() ,
,
sin∠ABF=![]() =
=![]() ,
,
在Rt△DBE中,sin∠DBE=![]() ,
,
∵∠ABF=∠DBE,
∴sin∠DBE=![]() ,
,
∴DE=BDsin∠DBE=![]() ×4
×4![]() =6(km),
=6(km),
∴景点D向公路a修建的这条公路的长约是6km;
(2)由题意可知∠CDB=75°,
由(1)可知sin∠DBE=![]() ,所以∠DBE=60°,
,所以∠DBE=60°,
∴∠DCB=180°75°60°=45°,
在Rt△DCE中,CE=DE=6 (km),
在Rt△DBE中, ∠BDE=75°-45°=30°,
∴BE=![]() BD=
BD=![]() (km),
(km),
∴BC=6+![]() (km)
(km)
∴景点B与景点C之间的距离为6+![]() km.
km.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
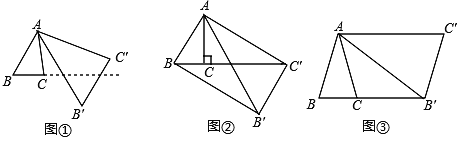
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′ ,如图①所示,∠BAB′ =θ, ![]() ,我们将这种变换记为[θ,n] .
,我们将这种变换记为[θ,n] .
(1)如图①,对△ABC作变换[60°,![]() ]得到△AB′C′ ,则
]得到△AB′C′ ,则![]() :
:![]() = ;直线BC与直线B′C′所夹的锐角为 度;
= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、![]() 在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
在同一直线上,且四边形ABB′C′为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得到△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,以下结论:
的图象如图所示,以下结论:
①常数m<﹣1;
②在每个象限内,y随x的增大而增大;
③若点A(﹣1,h),B(2,k)在图象上,则h<k;
④若点P(x,y)在上,则点P′(﹣x,﹣y)也在图象.
其中正确结论的个数是( )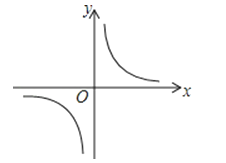
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
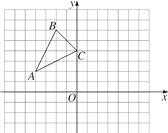
【题目】如图,已知A(-4,2),B(-2,6),C(0,4)是直角坐标系中的三点.
(1)把△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,画出平移后的图形,并写出点A的对应点A1的坐标;
(2)以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2,请在所给的坐标系中作出所有满足条件的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象在一,三象限.
(m为常数)的图象在一,三象限.
(1)求m的取值范围;
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,4),(﹣3,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为多少?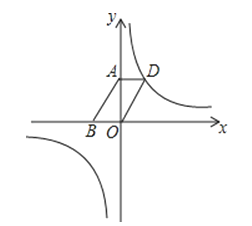
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人参加射击训练,每人各射击20次,他们射击成绩的平均数都是9.1环,各自的方差见如下表格:
甲 | 乙 | 丙 | 丁 | |
方差 | 0.293 | 0.375 | 0.362 | 0.398 |
由上可知射击成绩最稳定的是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:

如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面相同的纸牌A、B、C、D,其正面分别画有四个不同的几何图形(如图).小华将这4张纸牌背面朝上洗匀后任意摸出两张.

(1)用树状图(或列表法)表示所摸的两张牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张牌的牌面图形一定能组合成轴对称图形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com