

分析 (1)利用正方形得到条件,判断出△ADG≌△ABE,根据全等三角形的性质即可得到结论;
(2)利用正方形的性质在Rt△AMD中,∠MDA=45°,AD=2从而得出AM=DM=$\sqrt{2}$,在Rt△AMG中,AM2+GM2=AG2从而得出GM=$\sqrt{7}$即可.
解答 (1)如图1,延长EB交DG于点H,
∵四边形ABCD与四边形AEFG是正方形,
∴AD=AB,∠DAG=∠BAE=90°,AG=AE
在△ADG与△ABE中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAG=∠BAE}\\{AG=AE}\end{array}\right.$,
∴△ADG≌△ABE(SAS),
∴∠AGD=∠AEB,
∵△ADG中∠AGD+∠ADG=90°,
∴∠AEB+∠ADG=90°,
∵△DEH中,∠AEB+∠ADG+∠DHE=180°,
∴∠DHE=90°,
∴DG⊥BE;
(2)如图2,过点A作AM⊥DG交DG于点M,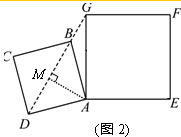
∠AMD=∠AMG=90°,
∵BD是正方形ABCD的对角,
∴∠MDA=45°
在Rt△AMD中,
∵∠MDA=45°,AD=2,
∴AM=DM=$\sqrt{2}$,
在Rt△AMG中,
∵AM2+GM2=AG2
∴GM=$\sqrt{7}$,
∵DG=DM+GM=$\sqrt{2}$+$\sqrt{7}$,
∴S△ADG=$\frac{1}{2}$DG•AM=$\frac{1}{2}$($\sqrt{2}$+$\sqrt{7}$)$\sqrt{2}$=1+$\frac{1}{2}$$\sqrt{14}$.
点评 此题考查了旋转的性质和正方形的性质,用到的知识点是旋转的性质、全等三角形的判定,勾股定理和正方形的性质,关键是根据题意画出辅助线,构造直角三角形.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄 | 12岁 | 13岁 | 14岁 | 15岁 |
| 人数 | 3人 | 4人 | 5人 | 1人 |
| A. | 12,13 | B. | 14,13 | C. | 12,13.5 | D. | 14,13.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:
为弘扬中华传统文化,了解学生整体听写能力,某校组织全校1000名学生进行一次汉字听写大赛初赛,从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制出了频数分布表和频数分布直方图:| 分组/分 | 频数 | 频率 |
| 50≤x<60 | 6 | 0.12 |
| 60≤x<70 | a | 0.28 |
| 70≤x<80 | 16 | 0.32 |
| 80≤x<90 | 10 | 0.20 |
| 90≤x≤100 | c | b |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=4,AB=3,则线段CE的长度是( )
已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=4,AB=3,则线段CE的长度是( )| A. | $\frac{25}{8}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 2.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com