
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P (x��y)������Q������Ϊ(ax+y��x+ay)�� ����aΪ��������Ƶ�Q�ǵ�P����a��������"�����磬��P(1��4)����3��������"ΪQ (3��1+4��1+3��4)�� ��Q (7��13)��

(1)��֪��A (-2��6)����![]() �����������ǵ�A1����B����2������������B1 (3�� 3)�� ���A1�͵�B�����꣺
�����������ǵ�A1����B����2������������B1 (3�� 3)�� ���A1�͵�B�����꣺
(2)��֪��M (m-1�� 2m)����-3��������"Mλ���������ϣ���M������
���𰸡���1��A1 (5�� 1)��![]() ����2��
����2��![]() (
(![]() ��0)��
��0)��![]() (0��-16).
(0��-16).
��������
��1�����ݹ�����Ķ��壬��ϵ�����꼴�ɵó����ۣ�
��2���ȱ�ʾ����M��m-1��2m���ġ�-3�������㡱M�䣬Ȼ������������⼴�����M������꣮
(1) ����A(-2�� 6)����![]() �����������ǵ�A��
�����������ǵ�A��
��A (![]() ��
��![]() )�� ��A1 (5�� 1).
)�� ��A1 (5�� 1).
���B(x�� y)��
����B����2��������"��B (3�� 3)��
��![]() ��
��
���![]() ����
����![]() ��
��
(2) ����M(m-1�� 2m) ����- 3����������ΪM (-3 (m-1) +2m�� m-1+ (-3) ��2m)����![]() (-m+3�� -5m-1)��
(-m+3�� -5m-1)��
��![]() λ��x���ϣ�.m-1-6m= =0��ã�
λ��x���ϣ�.m-1-6m= =0��ã�![]() ��
��
��-3 (m-1) +2m=![]() ��
��
![]() ��
��
��![]() λ��y���ϣ���.-3 (m-1) +2m=0����ã� m=3��
λ��y���ϣ���.-3 (m-1) +2m=0����ã� m=3��
��![]() ��
��![]() .
.
����������![]() ��������
��������![]() (
(![]() ��0)��
��0)��![]() (0��-16).
(0��-16).


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �Ľ�ƽ���ߣ�
�Ľ�ƽ���ߣ�![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ������ֱ���60��40����
������ֱ���60��40����![]() �����( )
�����( )

A.8B.10C.12D.20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=2����BAD=60��������D��DE��AB�ڵ�E��DF��BC�ڵ�F������EDF�Ե�DΪ��ת������ת��������DE�䣬DF���ֱ���ֱ��AB��BC�ཻ�ڵ�G��P������GP������DGP���������3![]() ʱ������ת�ǵĴ�С��ָ����ת����
ʱ������ת�ǵĴ�С��ָ����ת����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
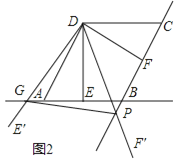
����Ŀ����ͼ1����ABC����DCE��Ϊ�ȱ������Σ���B��C��E������ͬһ��ֱ����ʱ������BD��AE���ڵ�F����֤����ACE�ա�BCD.������С������DCE�Ƶ�C��ת�Ĺ����з�����һЩ����Ľ��ۣ�������һ����С����̽��֮�ã�

��̽��һ����ͼ2����B��C��E���㲻��ͬһ��ֱ����ʱ��С�����֡�BFE�Ĵ�Сû�з����仯��������������BFE�Ķ�����

��̽�������Ķ����ϣ���ƽʱ����ϰ�У�������̽���õ�����һ����ȷ�Ľ��ۣ�����ȫ�������εĶ�Ӧ���ϵĸ����.���磺��ͼ3�������ABC�ա�A��B��C����AD��A��D���ֱ�����ABC����A��B��C���ı�BC��B��C���ϵĸߣ���ô����֤��AD=A��D��.С������������˼���������µķ��֣���ͼ4��������CF����CFƽ�֡�BFE���������˵�����ɣ�

��̽��������̽�����Ļ����ϣ�С���ֽ�һ���о����֣��߶�AF��BF��CF֮�仹����һ����������ϵ������д������֮��Ĺ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Լ����μ��п���5000�����б�ҵ��������һ�������������飬���Ƴ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��һ���֣�
�����ͼ����Ϣ�ش��������⣺
���� | Ƶ�����ˣ� | Ƶ�� |
4.0��x��4.3 | 20 | 0.1 |
4.3��x��4.6 | 40 | 0.2 |
4.6��x��4.9 | 70 | 0.35 |
4.9��x��5.2 | a | 0.3 |
5.2��x��5.5 | 10 | b |
��1�����ε��������Ϊ________����������Ϊ_______��
��2����Ƶ���ֲ����У�a=______��b=______������Ƶ���ֲ�ֱ��ͼ����������
��3����������4.6���ϣ���4.6����������������������Ϣ����ȫ�����б�ҵ��������������ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪E��F�ֱ�Ϊ������ABCD�ı�AB��BC���е㣬AF��DE���ڵ�M��OΪBD���е㣬�����н��ۣ�
�١�AME=90�㣻�ڡ�BAF=��EDB���ۡ�BMO=90�㣻��MD=2AM=4EM����AM=![]() MF��������ȷ���۵��ǣ�������
MF��������ȷ���۵��ǣ�������

A. �٢ۢ� B. �ڢܢ� C. �٢ۢܢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
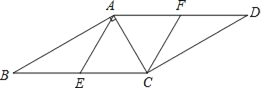
����Ŀ����ͼ����֪��E��F�ֱ���ABCD�ı�BC��AD�ϵ��е㣬����BAC=90��������B=30�㣬BC=10�����ı���AECF�����Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x��3����x��2��=|m|��
��1����֤����������ʵ��m������������������ȵ�ʵ������
��2�������̵�һ������1����m��ֵ�����̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����λ������ǧλ�������λ����֮��Ϊx��ʮλ�������λ����֮��Ϊy�����x=y����ô�������λ��Ϊ��ƽ������.
��1����С�ġ�ƽ������Ϊ ����λ��A��4738֮��Ϊ���ġ�ƽ����������A��ֵΪ_______��
��2��һ����λ��ƽ������M�����ĸ�λ������ǧλ����a��3������λ����b��ʮλ����֮��Ϊ8������������������ġ�ƽ������M��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com