
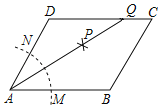
【题目】如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;
MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成如图表(成绩得分均为整数):
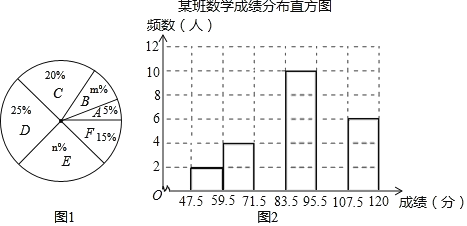

根据图表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ;扇形统计图中的m= ,n= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 人,72分及以上为及格,预计及格的人数约为 人;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
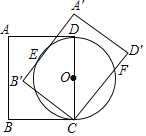
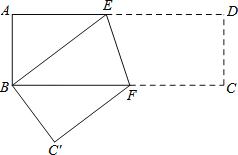
【题目】如图,在矩形ABCD中,AB=5,BC=4,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,边CD′与⊙O相交于点F,则CF的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
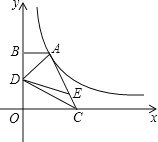
【题目】如图,点A在双曲线y=![]() (k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
(k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4cm,AD=8cm,按如图方式折叠,使点D与点B重合,折痕为EF,则tan∠BEF=( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,AD=4cm,EF经过对角线BD的中点O,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE;
(2)当EF⊥BD时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
概念理解:将△ABC 绕点 A 按逆时针方向旋转,旋转角记为 θ(0°≤θ≤90°),并使各边长变为原来的 n 倍,得到△AB′C′,如图,我们将这种变换记为[θ,n],![]() :
:![]() .
.

问题解决:(2)如图,在△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得到△AB′C′,使点 B,C,C′在同一直线上,且四边形 ABB′C′为矩形,求 θ 和 n 的值.

拓广探索:(3)在△ABC 中,∠BAC=45°,∠ACB=90°,对△ABC作变换 得到△AB′C′,则四边形 ABB′C′为正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com