
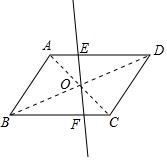
 观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?
观察发现:直线l在绕点O旋转的过程中,①以E、F为端点的线段中,哪些线段的长度发生了变化?分析 ①观察图形得到线段OE、OF、AE、CF、DE、BF的长度发生了变化;
②在旋转的过程中,OE与OF相等;以E、F为端点的线段中还具有相等关系的线段有:AE=CF,DE=BF;
③利用平行四边形的性质得OA=OC,AD=BC,AB=CD,AD∥BC,则∠EAO=∠FCO,于是可证明△AEO≌△CFO,所以AE=CF,S△AEO=S△COF,则DE=BF,易得四边形ABFE和四边形CDEF的周长相等,它们的面积相等.
解答 解:①以E、F为端点的线段中,线段OE、OF、AE、CF、DE、BF的长度发生了变化;
②在旋转的过程中,OE与OF相等;以E、F为端点的线段中还具有相等关系的线段有:AE=CF,DE=BF;
③在旋转的过程中,平行四边形被分成的两部分的面积和周长相等.
证明如下:
∵四边形ABCD为平行四边形,
∴OA=OC,AD=BC,AB=CD,AD∥BC,
∴∠EAO=∠FCO,
在△AEO和△CFO中
$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{AO=CO}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AEO≌△CFO,
∴AE=CF,S△AEO=S△COF,
∴DE=BF,
∴四边形ABFE和四边形CDEF的周长相等,它们的面积相等.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了平行四边形的性质.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 0 | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
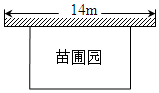 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为14米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为14米(如图所示),设这个苗圃园垂直于墙的一边长为x米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com