
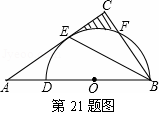
如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边
上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA= ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
 |
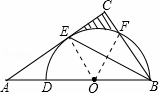
解:(1)连接OE.
∵OB=OE ∴∠OBE=∠OEB
 ∵BE是△ABC的角平分线 ∴∠OBE=∠EBC
∵BE是△ABC的角平分线 ∴∠OBE=∠EBC
∴∠OEB=∠EBC ∴OE∥BC
∵∠C=90° ∴∠AEO=∠C=90°
∴AC是⊙O的切线;
(2)连接OF.
∵sinA=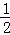 ,∴∠A=30° ∵⊙O的半径为4,∴AO=2OE=8,
,∴∠A=30° ∵⊙O的半径为4,∴AO=2OE=8,
∴AE=4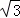 ,∠AOE=60°,∴AB=12, ∴BC=
,∠AOE=60°,∴AB=12, ∴BC=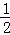 AB=6 AC=6
AB=6 AC=6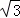 ,
,
∴CE=AC﹣AE=2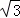 .
.
∵OB=OF,∠ABC=60°,∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,∴∠EOF=60°.
∴S梯形OECF=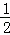 (2+4)×2
(2+4)×2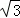 =6
=6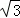 .
.
S扇形EOF=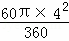 =
=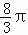
∴S阴影部分=S梯形OECF﹣S扇形EOF=6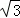 ﹣
﹣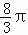 .
.


科目:初中数学 来源: 题型:
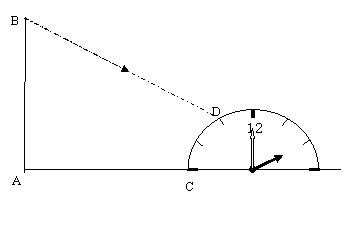
萧山区人民广场旗杆AB旁边有一个半圆的时钟模型,如图,时钟的9点和3点的刻度线刚好和地面重合,半圆的半径2米,旗杆的底端A到钟面9点刻度C的距离为5米,一天小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得一米长的标杆的影长1.6米,求旗杆AB的高度?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线y=mx与双曲线y=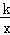 交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )
交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=4,则k的值为( )
A.-2 B.-4 C.4 D.-8
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
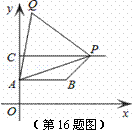
如图,已知点A(0,2)、B(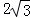 ,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
,2)、C(0,4),过点C向右作平行于x轴的射线,点P是射线上的动点,连接AP,以AP为边在其左侧作等边△APQ,连接PB、BA.若四边形ABPQ为梯形,则:
(1)当AB为梯形的底时,点P的横坐标是 ;
(2)当AB为梯形的腰时,点P的横坐标是 .
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
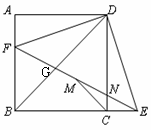
如图,正方形ABCD中, F为AB上一点,E是BC延长线上一点,且AF=EC,连结EF,DE,DF,M是FE中点,连结MC,设FE与DC相交于点N。则4个结论:①∠EDF=90°;②△BFG∽△EDG∽△BDE;③AD2+AF2=DG×DB;④若MC=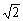 ,则BF=2;正确的结论有( )
,则BF=2;正确的结论有( )
A、① ② B、①②③ C、③④ D、①②③④
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,∠AOB=90°,OA=OB=10,分别以边OA、OB所在的直线为坐标轴建立平面直角坐标系,点P自点A出发沿线段AB匀速运动至点B停止。同时点D自原点O出发沿x轴正方向匀速运动。在点P、D运动的过程中,始终满足PO=PD,过点O、D向AB做垂线,垂足分别为点C、E,设OD=x
(1)AP=(用含x的代数式表示)
(2)在点P、D运动的过程中,线段PC与BE是否相等?若相等,请给予证明,若不相等,说明理由。
 (3)设以点P、O、D、E为顶点的四边形面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围。
(3)设以点P、O、D、E为顶点的四边形面积为y,请直接写出y与x的函数关系式,并写出自变量的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com