
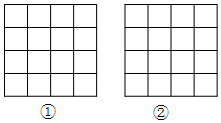
 (1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);
(1)比较大小:$\sqrt{5}$+1>$\sqrt{10}$(填“>”、“<”或者“=”);分析 (1)直接利用$\sqrt{5}$,$\sqrt{10}$的近似值进而比较得出答案;
(2)直接利用勾股定理构造三角形进而得出答案;
(3)直接利用勾股定理构造三角形进而得出答案.
解答 解:(1)∵$\sqrt{5}$≈2.23,$\sqrt{10}$≈3.16,
∴$\sqrt{5}$+1>$\sqrt{10}$;
故答案为:>;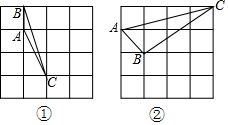
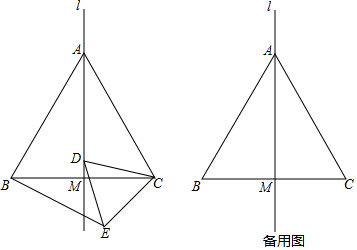
(2)如图①所示:
AB=1,AC=$\sqrt{5}$,BC=$\sqrt{10}$,
易得AB+AC>BC;
(3)“<”.如图②所示,
AB=$\sqrt{2}$,BC=$\sqrt{13}$,AC=$\sqrt{17}$,则AC-AB<BC.
故答案为:<.
点评 此题主要考查了应用设计与作图以及勾股定理,正确应用勾股定理是解题关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.
如图,正方形ABCD的边长为1,点E在边AB上,连接ED,过点D作FD⊥DE与BC的延长线相交于点F,连接EF与边CD相交于点G、与对角线BD相交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
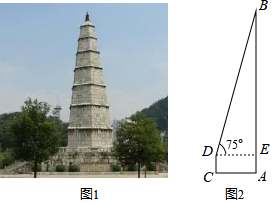 阅读材料:
阅读材料:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com