

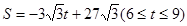 ;(3)存在,t=
;(3)存在,t=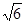 或t=
或t=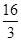 .
.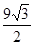 ,可求得AQ的长度,进而得到点Q的运动速度;
,可求得AQ的长度,进而得到点Q的运动速度;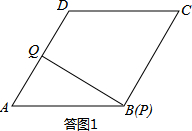
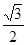 =
=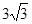 cm, S=S△APQ=
cm, S=S△APQ=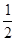 AQ•h=
AQ•h=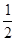 AQ×3
AQ×3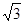 =
=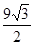 ,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示:
,解得AQ=3cm.∴点Q的运动速度为:3÷3=1cm/s.(2)由题意,可知题图2中FG段表示点P在线段CD上运动时的情形.如答图2所示: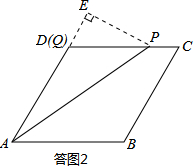
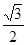 ,
,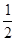 AD•PE=
AD•PE=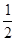 ×6×(?
×6×(?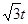 +
+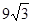 )=
)=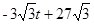 .
.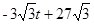 (6≤t≤9).
(6≤t≤9).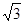 ,
,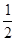 AQ•AP•sin60°=
AQ•AP•sin60°=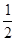 t•2t×
t•2t×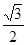 =
=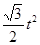 ,
,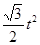 =
=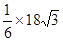 ,
,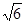 s,
s,
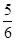 S菱形ABCD,即
S菱形ABCD,即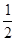 (2t-6+t)×6×
(2t-6+t)×6×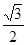 =
=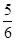 ×18
×18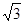 ,
,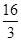 s,
s,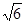 或
或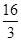 时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.
时,使PQ将菱形ABCD的面积恰好分成1:5的两部分.

 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
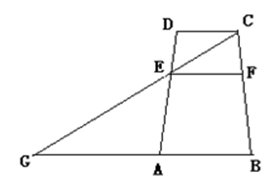
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

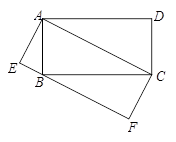
 ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,点P从B点出发,沿BC方向以2cm/m的速度移动,点Q从C出发,沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发,经过多少时间△CPQ与△CBA相似?
,点P从B点出发,沿BC方向以2cm/m的速度移动,点Q从C出发,沿CA方向以1cm/m的速度移动。若P、Q同时分别从B、C出发,经过多少时间△CPQ与△CBA相似?
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 AE,垂足为G,BG=
AE,垂足为G,BG= ,则△CEF的周长为( )
,则△CEF的周长为( )
| A.8 | B.9.5 | C.10 | D.11.5 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
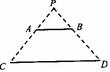
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com