
ΓΨΧβΡΩΓΩ»γΆΦΔΌ“―÷ΣœΏΕΈCDΥυ‘Ύ÷±œΏΒΡΫβΈω ΫΈΣyΘΫ©¹![]() x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
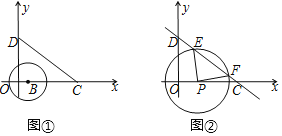
Θ®1Θ©»τ“‘ΒψBΘ®1Θ§0Θ©ΈΣ‘≤–ΡΒΡΓ―BΑκΨΕΈΣrΘ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§‘ρr¬ζΉψΓΓ ΓΓΘ°
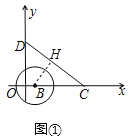
Θ®2Θ©»γΆΦΔΎΘ§»γΙϊΒψP¥”Θ®©¹5Θ§0Θ©≥ωΖΔΘ§“‘1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―Ίx÷αœρ”“Ής‘»ΥΌ‘ΥΕ·Θ§Β±‘ΥΕ· ±ΦδΒΫtΟκ ±Θ§“‘ΒψPΈΣ‘≤–ΡΓΔ![]() tΗωΒΞΈΜ≥ΛΕ»ΈΣΑκΨΕΒΡ‘≤P”κœΏΕΈCDΥυ‘Ύ÷±œΏ”–ΝΫΗωΫΜΒψΘ§Ζ÷±πΈΣΒψEΓΔFΘ§«“ΓœEPFΘΫ2ΓœOCDΘ§«σ¥Υ ±tΒΡ÷ΒΘ°
tΗωΒΞΈΜ≥ΛΕ»ΈΣΑκΨΕΒΡ‘≤P”κœΏΕΈCDΥυ‘Ύ÷±œΏ”–ΝΫΗωΫΜΒψΘ§Ζ÷±πΈΣΒψEΓΔFΘ§«“ΓœEPFΘΫ2ΓœOCDΘ§«σ¥Υ ±tΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©rΘΫ![]() Μρ3ΘΦrΓή
Μρ3ΘΦrΓή![]() ΘΜΘ®2Θ©tΘΫ
ΘΜΘ®2Θ©tΘΫ![]() sΜρ
sΜρ![]() s ±Θ§¬ζΉψΧθΦΰΘ°
s ±Θ§¬ζΉψΧθΦΰΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷ΝΫ÷÷«ι–ΈΘΚΔΌœύ«–ΘΜΔΎ”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§Ζ÷±π«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©Ζ÷ΝΫ÷÷«ι–ΈΖ÷±πΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©»γΆΦΔΌ÷–Θ§ΉςBHΓΆCD”ΎHΘ°
ΓΏ÷±œΏyΘΫ©¹![]() x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
x+3Θ§Ζ÷±πΫΜΉχ±ξ÷α”ΎΒψCΓΔDΘ§
ΓύCΘ®4Θ§0Θ©Θ§DΘ®0Θ§3Θ©Θ§
ΓύODΘΫ3Θ§OCΘΫ4Θ§
ΓύCDΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
ΓΏBΘ®1Θ§0Θ©Θ§
ΓύOBΘΫ1Θ§BCΘΫ3Θ§
ΓΏΓœBCHΘΫΓœDCOΘ§ΓœBHCΘΫΓœCODΘΫ90ΓψΘ§
ΓύΓςBCHΓΉΓςDCOΘ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
Γύ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύBHΘΫ![]() Θ§
Θ§
ΓύΒ±rΘΫ![]() ±Θ§÷±œΏCD”κΓ―Bœύ«–Θ§÷Μ”–“ΜΗωΫΜΒψΘ§
±Θ§÷±œΏCD”κΓ―Bœύ«–Θ§÷Μ”–“ΜΗωΫΜΒψΘ§
ΓΏBDΘΫ![]() ΘΫ
ΘΫ![]() Θ§
Θ§
ΓύΒ±3ΓήrΘΦ![]() ±Θ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§
±Θ§Γ―B”κœΏΕΈCD÷Μ”–“ΜΗωΫΜΒψΘ§
Ι ¥πΑΗΈΣΘΚrΘΫ![]() Μρ3ΘΦrΓή
Μρ3ΘΦrΓή![]() Θ°
Θ°
Θ®2Θ©ΔΌ»γΆΦΔΎ÷–Θ§Β±ΒψP‘ΎœΏΕΈOC…œ ±Θ§ΉςPHΓΆEF”ΎHΘ°
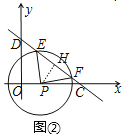
ΓΏΓœEPFΘΫ2ΓœOCDΘ§
ΓΏPEΘΫPFΘ§PHΓΆEFΘ§
ΓύΓœEPHΘΫΓœFPHΘ§
ΓύΓœHPFΘΫΓœOCDΘ§
ΓΏPFΘΫ![]() tΘ§
tȧ
ΓύPHΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
PCΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
Γύt+![]() tΘΫ9Θ§
tΘΫ9Θ§
ΓύtΘΫ![]() Θ°
Θ°
ΔΎ»γΆΦΔΎ©¹1÷–Θ§Β±ΒψP‘ΎOC ΒΡ―”≥ΛœΏ…œ ±Θ§ΉςPHΓΆEF”ΎHΘ°
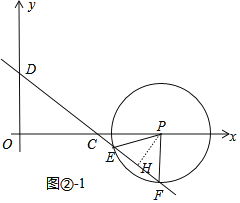
Ά§Ζ®Ω…÷ΣPFΘΫ![]() tΘ§PHΘΫ
tΘ§PHΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§PCΘΫ
tΘ§PCΘΫ![]() t
t![]() ΘΫ
ΘΫ![]() tΘ§
tȧ
Ω…ΒΟΘΚtΘΫ![]() t+9Θ§
t+9Θ§
tΘΫ![]()
Ήέ…œΥυ ωΘ§tΘΫ![]() sΜρ
sΜρ![]() s ±Θ§¬ζΉψΧθΦΰΘ°
s ±Θ§¬ζΉψΧθΦΰΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§≈ΉΈοœΏyΘΫax2+bx©¹4Ψ≠ΙΐΒψAΘ®©¹8Θ§0Θ©Θ§Ε‘≥Τ÷α «÷±œΏxΘΫ©¹3Θ§ΒψB «≈ΉΈοœΏ”κy÷αΫΜΒψΘ§ΒψMΓΔNΆ§ ±¥”‘≠ΒψO≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»Ζ÷±π―Ίx÷αΒΡΗΚΑκ÷αΓΔyΒΡΗΚΑκ÷αΖΫœρ‘»ΥΌ‘ΥΕ·Θ§Θ®Β±ΒψNΒΫ¥οΒψB ±Θ§ΒψMΓΔNΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ©Θ°ΙΐΒψMΉςx÷αΒΡ¥ΙœΏΘ§ΫΜ÷±œΏAB”ΎΒψCΘ§Ν§Ϋ”CNΓΔMNΘ§≤ΔΉςΓςCMNΙΊ”Ύ÷±œΏMCΒΡΕ‘≥ΤΆΦ–ΈΘ§ΒΟΒΫΓςCMDΘ°…ηΒψN‘ΥΕ·ΒΡ ±ΦδΈΣtΟκΘ§ΓςCMD”κΓςAOB÷ΊΒΰ≤ΩΖ÷ΒΡΟφΜΐΈΣSΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΘΜ
Θ®2Θ©Β±0ΘΦtΘΦ2 ±Θ§
ΔΌ«σS”κtΒΡΚ· ΐΙΊœΒ Ϋ.
ΔΎ÷±Ϋ”–¥≥ωΒ±tΘΫ_____ ±Θ§ΥΡ±Ώ–ΈCDMNΈΣ’ΐΖΫ–Έ.
Θ®3Θ©Β±ΒψD¬δ‘Ύ±ΏAB…œ ±Θ§ΙΐΒψCΉς÷±œΏEFΫΜ≈ΉΈοœΏ”ΎΒψEΘ§ΫΜx÷α”ΎΒψFΘ§Ν§Ϋ”EBΘ§Β±SΓςCBEΘΚSΓςACFΘΫ1ΘΚ3 ±Θ§÷±Ϋ”–¥≥ωΒψEΒΡΉχ±ξΈΣ______Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
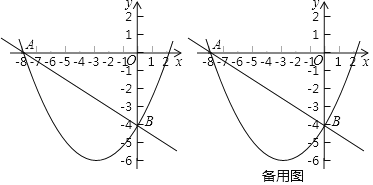
ΓΨΧβΡΩΓΩ“―÷ΣΕΰ¥ΈΚ· ΐyΘΫax2+bx+cΒΡΆΦœσ»γΆΦΥυ ΨΘ§Υϋ”κx÷αΒΡΝΫΗωΫΜΒψΒΡΉχ±ξΖ÷±πΈΣ(©¹1Θ§0)Θ§(3Θ§0)Θ§«“ΒψP1(x1Θ§y1)ΓΔP2(x2Θ§y2)‘Ύ¥Υ≈ΉΈοœΏ…œΘ°Ε‘”Ύœ¬Ν–Ϋα¬έΘΚΔΌabcΘΨ0ΘΜΔΎb2©¹4acΘΨ0ΘΜΔέΒ±x1ΘΦx2ΘΦ0 ±Θ§y1ΘΨy2ΘΜΔήΒ±©¹1ΘΦxΘΦ3 ±Θ§yΘΦ0Θ°Τδ÷–’ΐ»ΖΒΡ «_____(Χν–ρΚ≈)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ“ΜΗω≤ΜΆΗΟςΒΡΩΎ¥ϋ÷–ΉΑ”–3Ηω¥χΚ≈¬κΒΡ«ρΘ§«ρΚ≈Ζ÷±πΈΣ2Θ§3Θ§4Θ§’β–©«ρ≥ΐΚ≈¬κ≤ΜΆ§ΆβΤδΥϋΨυœύΆ§ΓΘΦΉΓΔ““ΓΔΝΫΆ§―ßΆφΟΰ«ρ”ΈœΖΘ§”ΈœΖΙφ‘ρ»γœ¬ΘΚ
œ»”…ΦΉΆ§―ߥ”÷–ΥφΜζΟΰ≥ω“Μ«ρΘ§Φ«œ¬«ρΚ≈Θ§≤ΔΖ≈ΜΊΫΝ‘»Θ§‘Ό”…““Ά§―ߥ”÷–ΥφΜζΟΰ≥ω“Μ«ρΘ§Φ«œ¬«ρΚ≈ΓΘΫΪΦΉΆ§―ßΟΰ≥ωΒΡ«ρΚ≈ΉςΈΣ“ΜΗωΝΫΈΜ ΐΒΡ °ΈΜ…œΒΡ ΐΘ§““Ά§―ßΒΡΉςΈΣΗωΈΜ…œΒΡ ΐΓΘ»τΗΟΝΫΈΜ ΐΡή±Μ4’ϊ≥ΐΘ§‘ρΦΉ ΛΘ§Ζώ‘ρ““ Λ.
Έ ΘΚ’βΗω”ΈœΖΙΪΤΫ¬πΘΩ«κΥΒΟςάμ”…ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
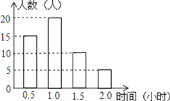
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΫβ»Ϊ–Θ2000Οϊ―ß…ζΒΡΩΈΆβ‘ΡΕΝ«ιΩωΘ§‘Ύ»Ϊ–ΘΖΕΈßΡΎΥφΜζΒς≤ιΝΥ50Οϊ―ß…ζΘ§ΒΟΒΫΥϊΟ«‘ΎΡ≥“ΜΧλΗςΉ‘ΩΈΆβ‘ΡΕΝΥυ”Ο ±ΦδΒΡ ΐΨίΘ§ΫΪΫαΙϊΜφ÷Τ≥…ΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ®»γΆΦΥυ ΨΘ©Θ°
Θ®1Θ©«κΖ÷±πΦΤΥψ’β50Οϊ―ß…ζ‘Ύ’β“ΜΧλΩΈΆβ‘ΡΕΝΥυ”Ο ±ΦδΒΡ÷Ύ ΐΓΔ÷–ΈΜ ΐΚΆΤΫΨυ ΐΘΜ
Θ®2Θ©«κΡψΗυΨί“‘…œΒς≤ιΘ§ΙάΦΤ»Ϊ–Θ―ß…ζ÷–‘Ύ’β“ΜΧλΩΈΆβ‘ΡΕΝΥυ”Ο ±Φδ‘Ύ1.0–Γ ±“‘…œΘ®Κ§1.0–Γ ±Θ©ΒΡ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“‘ΒψCΈΣΉχ±ξ‘≠ΒψΘ§Βψ![]() Θ§
Θ§![]() Θ§ΫΪ
Θ§ΫΪ![]() »ΤΒψAΥ≥ ±’κ–ΐΉΣ90ΓψΘ°
»ΤΒψAΥ≥ ±’κ–ΐΉΣ90ΓψΘ°
Θ®1Θ©‘ΎΆΦ÷–Μ≠≥ω–ΐΉΣΚσΒΡ![]() Θ§≤Δ–¥≥ωΒψ
Θ§≤Δ–¥≥ωΒψ![]() ΓΔ
ΓΔ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®2Θ©“―÷ΣΒψ![]() Θ§‘Ύx÷α…œ«σΉς“ΜΒψPΘ®ΉΔΘΚ≤Μ“Σ«σ–¥≥ωPΒψΒΡΉχ±ξΘ©Θ§ ΙΒΟPDΒΡ÷ΒΉν–ΓΘ§≤Δ«σ≥ω
Θ§‘Ύx÷α…œ«σΉς“ΜΒψPΘ®ΉΔΘΚ≤Μ“Σ«σ–¥≥ωPΒψΒΡΉχ±ξΘ©Θ§ ΙΒΟPDΒΡ÷ΒΉν–ΓΘ§≤Δ«σ≥ω![]() ΒΡΉν–Γ÷ΒΘΜ
ΒΡΉν–Γ÷ΒΘΜ
Θ®3Θ©–¥≥ω![]() ‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§œΏΕΈAB…®ΙΐΒΡΟφΜΐ
‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§œΏΕΈAB…®ΙΐΒΡΟφΜΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§…»–ΈOABΒΡΑκΨΕOA=3Θ§‘≤–ΡΫ«ΓœAOB=90ΓψΘ§ΒψC «ΜΓAB…œ“λ”ΎAΓΔBΒΡΕ·ΒψΘ§ΙΐΒψCΉςCDΓΆOA”ΎΒψDΘ§ΉςCEΓΆOB”ΎΒψEΘ§Ν§ΫαDEΘ§ΒψGΓΔH‘ΎœΏΕΈDE…œΘ§«“DG=GH=HE
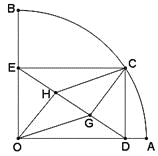
Θ®1Θ©«σ÷ΛΘΚΥΡ±Ώ–ΈOGCH «ΤΫ––ΥΡ±Ώ–ΈΘΜ
Θ®2Θ©Β±ΒψC‘ΎΜΓAB…œ‘ΥΕ· ±Θ§‘ΎCDΓΔCGΓΔDG÷–Θ§ «Ζώ¥φ‘Ύ≥ΛΕ»≤Μ±δΒΡœΏΕΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΗΟœΏΕΈΒΡ≥ΛΕ»ΘΜ
Θ®3Θ©«σ÷ΛΘΚ![]() «Ε®÷Β.
«Ε®÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΨΊ–Έ![]() ÷–Θ§
÷–Θ§![]() «Ε‘Ϋ«œΏΘ§Βψ
«Ε‘Ϋ«œΏΘ§Βψ![]() ΈΣΨΊ–ΈΆβ“ΜΒψ«“¬ζΉψ
ΈΣΨΊ–ΈΆβ“ΜΒψ«“¬ζΉψ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ”Ύ
”Ύ![]() Θ°
Θ°
Θ®1Θ©»τ![]() Θ§
Θ§![]() Θ§«σΨΊ–Έ
Θ§«σΨΊ–Έ![]() ΒΡΟφΜΐΘΜ
ΒΡΟφΜΐΘΜ
Θ®2Θ©»τ![]() Θ§ ‘≈–ΕœœΏΕΈ
Θ§ ‘≈–ΕœœΏΕΈ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ÷°ΦδΒΡΙΊœΒΘ§≤Δ÷ΛΟςΘ°
÷°ΦδΒΡΙΊœΒΘ§≤Δ÷ΛΟςΘ°
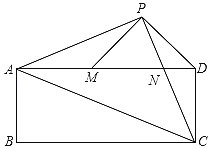
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCD÷–Θ§BEΤΫΖ÷ΓœDBC«“ΫΜCD±Ώ”ΎΒψEΘ§ΫΪΓςBCE»ΤΒψCΥ≥ ±’κ–ΐΉΣΒΫΓςDCFΒΡΈΜ÷ΟΘ§≤Δ―”≥ΛBEΫΜDF”ΎΒψGΘ°
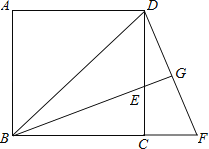
Θ®1Θ©«σ÷ΛΘΚΓςBDGΓΉΓςDEGΘΜ
Θ®2Θ©»τEGBG=4Θ§«σBEΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com