
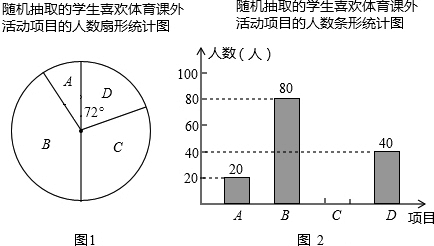
分析 (1)由题意可知这次被调查的学生共有40÷$\frac{72}{360}$=200;
(2)首先求得C项目对应人数为:200-20-80-40=60(人),继而可补全条形统计图;
(3)由题意可得喜欢排球人数所占扇形圆心角的大小为:$\frac{20}{200}$×360°=36°;
(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好选中乙、丙两位同学的情况,再利用概率公式即可求得答案.
解答  解:(1)根据题意得:这次被调查的学生共有40÷$\frac{72}{360}$=200(人);
解:(1)根据题意得:这次被调查的学生共有40÷$\frac{72}{360}$=200(人);
故答案为:200;
(2)C项目对应人数为:200-20-80-40=60(人);
补充如图.
(3)喜欢排球人数所占扇形圆心角的大小为:$\frac{20}{200}$×360°=36°;
(4)列表如下:
| 甲 | 乙 | 丙 | 丁 | |
| 甲 | ﹨ | (乙,甲) | (丙,甲) | (丁,甲) |
| 乙 | (甲,乙) | ﹨ | (丙,乙) | (丁,乙) |
| 丙 | (甲,丙) | (乙,丙) | ﹨ | (丁,丙) |
| 丁 | (甲,丁) | (乙,丁) | (丙,丁) | ﹨ |
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图的知识.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=-4 | B. | x=1 | C. | x1=4,x2=1 | D. | x1=-4,x2=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 144(1-x)2=100 | B. | 100(1-x)2=144 | C. | 144(1+x)2=100 | D. | 100(1+x)2=144 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com