
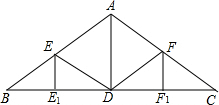
 已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.
已知:如图的房屋梁架中,AB=AC=4m,∠BAC=120°,点D、E、F分别是BC、AB、AC的中点,且EE1⊥BC,AD⊥BC,FF1⊥BC,求EE1,ED,AD,FD,FF1的长.| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案:
在淮南市发出创建文明城的倡议后,我校的小华与小明同学便积极的行动起来,他们在上体育课时发现操场上有块如图1所示的空地,经测量,在△ABC中,∠C=90°,AC=6m,BC=8m,他们向学校建议由他们来设计绿化方案:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空:
如图,l1反映了某公司产品的销售收入y1(元)与销售量x(吨)的关系,l2反映了该公司产品的销售成本y2(元)与销售量x(吨)之间的关系,根据图象填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com