
【题目】小林准备进行如下操作实验:把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?(求出剪成的两段铁丝的长度)
(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.
【答案】(1)较短的一段长为12cm,较长的一段长为28cm;(2)小峰的说法正确,这两个正方形的面积之和不可能等于48cm2
【解析】
(1)设剪成的较短的这段为xcm,较长的这段就为(40-x)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于58cm2建立方程求出其解即可;(2)设剪成的较短的这段为mcm,较长的这段就为(40-m)cm.就可以表示出这两个正方形的面积,根据两个正方形的面积之和等于48cm2建立方程,如果方程有解就说明小峰的说法错误,否则正确.
(1)设剪成的较短的一段长为xcm,则较长的一段长为(40-x)cm,
由题意,得![]() +
+![]() =58,
=58,
解得x1=12,x2=28.
当x=12时,较长的一段长为40-12=28(cm),
当x=28时,较长的一段长为40-28=12(cm)<28cm(舍去).
∴较短的一段长为12cm,较长的一段长为28cm.
(2)小峰的说法正确.理由如下:
设剪成的较短的一段长为m cm,则较长的一段长就为(40-m) cm,
由题意得![]() +
+![]() =48,
=48,
变形为m2-40m+416=0.
∵Δ=(-40)2-4×416=-64<0,
∴原方程无实数解,
∴小峰的说法正确,这两个正方形的面积之和不可能等于48cm2.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
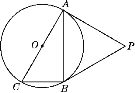
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=![]() ,∠ACB=60°,求⊙O的半径.
,∠ACB=60°,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
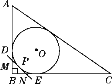
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】选择适当的方法解下列方程:
(1)(x-1)2+2x(x-1)=0;
(2)x2-6x-6=0;
(3)6 000(1-x)2=4 860;
(4)(10+x)(50-x)=800;
(5)(2x-1)2=x(3x+2)-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
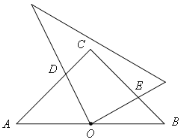
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AB=![]() cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
cm,将一块直角三角板的直角顶点放在点O处旋转,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE=______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,圆M经过原点O,直线![]() 与x轴、y轴分别相交于A,B两点.
与x轴、y轴分别相交于A,B两点.
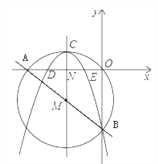
(1)求出A,B两点的坐标;
(2)若有一抛物线的对称轴平行于y轴且经过点M,顶点C在圆M上,开口向下,且经过点B,求此抛物线的函数解析式;
(3)设(2)中的抛物线交![]() 轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=
轴于D、E两点,在抛物线上是否存在点P,使得S△PDE=![]() S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
S△ABC?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店采购人员第一次用100元去采购“企鹅牌”玩具,很快售完,第二次去采购时发现批发价每件上涨了0.5元,用去了150元,所购玩具数量比第一次多了10件,两批玩具的售价均为2.8元,问:第二次采购玩具多少件?(说明:根据销售常识,批发价应该低于销售价)
查看答案和解析>>
科目:初中数学 来源: 题型:
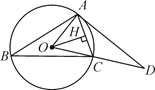
【题目】如图,△ABC内接于⊙O,OH⊥AC于点H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5![]() ,请求出:
,请求出:
(1)∠AOC的度数;
(2)劣弧![]() 的长;(结果保留π)
的长;(结果保留π)
(3)线段AD的长.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com