
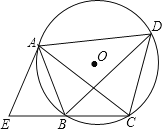
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,BA平分∠EBD,AE=AB.
(1)求证:AC=AD.
(2)当![]() ,AD=6时,求CD的长.
,AD=6时,求CD的长.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图,有四张背面完全相同的纸牌![]() ,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.
,其正面分别画有四个不同的几何图形,将这四张纸牌背面朝上洗匀.

(1)从中随机摸出一张,求摸出的牌面图形是中心对称图形的概率;
(2)小明和小亮约定做一个游戏,其规则为:先由小明随机摸出一张纸牌,不放回,再由小亮从剩下的纸牌中随机摸出一张,若摸出的两张牌面图形都是轴对称图形小明获胜,否则小亮获胜,这个游戏公平吗?请用列表法(或树状图)说明理由(纸牌用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每天可以销售
元,每天可以销售![]() 件,为尽快减少库存,商场决定降价促销.
件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件![]() 元,求两次下降的百分率;
元,求两次下降的百分率;
(2)经调查,若该商品每降价![]() 元,每天可多销售
元,每天可多销售![]() 件,
件,
①每天要想获得![]() 元的利润,每件应降价多少元?
元的利润,每件应降价多少元?
②能不能一天获得![]() 元的利润?请说明理由.
元的利润?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
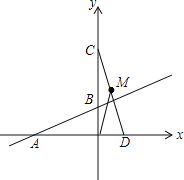
(1)点C的坐标是 ,线段AD的长等于 ;
(2)点M在CD上,且CM=OM,抛物线y=x2+bx+c经过点G,M,求抛物线的解析式;
(3)如果点E在y轴上,且位于点C的下方,点F在直线AC上,那么在(2)中的抛物线上是否存在点P,使得以C,E,F,P为顶点的四边形是菱形?若存在,请求出该菱形的周长l;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
x2+bx+c与x轴交于点A(﹣3,0)和点B,与y轴交于点C (0,2).
(1)求抛物线的表达式,并用配方法求出顶点D的坐标;
(2)若点E是点C关于抛物线对称轴的对称点,求tan∠CEB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2kx+![]() k2-2=0.
k2-2=0.
(1)求证:不论k为何值,方程总有两不相等实数根.
(2)设x1,x2是方程的根,且 x12-2kx1+2x1x2=5,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
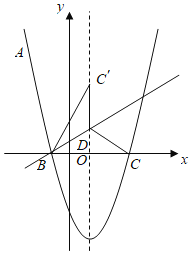
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,
两点,
(1)抛物线的函数表达式;
(2)点![]() 在抛物线的对称轴上,且位于
在抛物线的对称轴上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿沿直线
沿沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)设![]() 是抛物线上位于对称轴右侧的一点,点
是抛物线上位于对称轴右侧的一点,点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
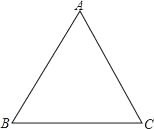
【题目】已知如图是边长为10的等边△ABC.
(1)作图:在三角形ABC中找一点P,连接PA、PB、PC,使△PAB、△PBC、△PAC面积相等.(不写作法,保留痕迹.)
(2)求点P到三边的距离和PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com