
【题目】如图,在菱形ABCD中,对角线AC,BD相交于点O,过点O作一条直线分别交DA,BC的延长线于点E,F,连接BE,DF.
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,![]() ,AE=2,求菱形ABCD的边长.
,AE=2,求菱形ABCD的边长.

【答案】(1)证明见解析;(2)6.
【解析】
(1)根据两直线平行,内错角相等可得∠AEO=∠CFO,然后利用“角角边”证明△AEO和△CFO全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相平分的四边形是平行四边形证明即可;
(2)设OM=x,BM=2x,根据△AOM∽△OBM,求得AM=![]() =
=![]() x,根据△AEM∽△BFM,求得EM:FM=AM:BM=
x,根据△AEM∽△BFM,求得EM:FM=AM:BM=![]() x:2x=
x:2x=![]() ,根据△AEM∽△BFM,求得结论.
,根据△AEM∽△BFM,求得结论.
(1)证明:在菱形ABCD中,AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AEO和△CFO中,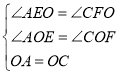 ,
,
∴△AEO≌△CFO(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形;
(2)解:∵![]() ,
,
∴设OM=x,BM=2x,
∵EF⊥AB,
又∵AC⊥BD,
∴∠AOM=∠OBM,
∴△AOM∽△OBM,
∴![]() =
=![]() ,
,
∴AM=![]() =
=![]() x,
x,
∵AD∥BC,
∴△AEM∽△BFM,
∴EM:FM=AM:BM=![]() x:2x=
x:2x=![]() ,
,
∵△AEO≌△CFO,
∴AE=CF,
∵AE∥BF,
∴△AEM∽△BFM,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴BF=8,
∴BC=6,
∴菱形ABCD的边长为6.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】“三等分角”是数学史上一个著名的问题,但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图):将给定的锐角∠AOB置于直角坐标系中,边OB在x轴上、边OA与函数![]() 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=![]() ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题:
(1)设P(![]() ,
,![]() )、R(
)、R(![]() ,
,![]() ),求直线OM对应的函数表达式(用含
),求直线OM对应的函数表达式(用含![]() ,
,![]() 的代数式表示);
的代数式表示);
(2)分别过点P和R作y轴和x轴的平行线,两直线相交于点Q.请说明Q点在直线OM上,并据此证明∠MOB=![]() ∠AOB;
∠AOB;
(3)应用上述方法得到的结论,你如何三等分一个钝角(用文字简要说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
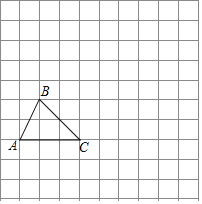
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)
(1)将△ABC向左平移1个单位,再向上平移5个单位件到△A1B1C1请画出△A1B1C1
(2)请在网格中将△ABC以A为位似中心放大3倍,得△AB2C2,请画出△AB2C2
(3)△A1B1C1和△AB2C2的面积比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图(1),在△ABC中,AB=BC=2CD,∠ABC=∠DCB=120°,AC交BD于点E.

(1)如图1:作BM⊥CA于M,求证:△DCE≌△BME;
(2)如图2:点F为BC中点,连接AF交BD于点G,当AB=a时,求线段FG的长度(用含a的代数式表示);
(3)如图3:在(2)的条件下,将△ABG沿AG翻折得到△AKG,延长AK交BD于点H,若BH=5![]() ,求CE的长.
,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
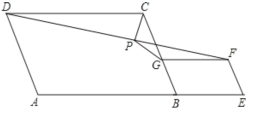
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A、 B、 E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
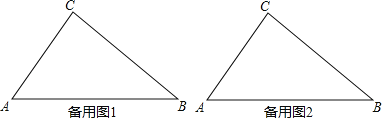
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发沿线段AB以每秒1cm的速度运动,同时点Q从点B出发沿折线B﹣C﹣A以每秒2cm的速度运动.其中一点停止则另一点也随之停止,设运动时间为t秒.
(Ⅰ)①直接写出t的取值范围: ;
②当点P运动到AB中点时,连结PQ,PC,BQ,求证:△CPQ∽△ABQ;
(Ⅱ)当△BPQ是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
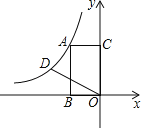
【题目】如图,矩形ABOC的顶点B、C分别在x轴,y轴上,顶点A在第二象限,点B的坐标为(﹣2,0).将线段OC绕点O逆时针旋转60°至线段OD,若反比例函数y=![]() (k≠0)的图象经过A、D两点,则k值为______.
(k≠0)的图象经过A、D两点,则k值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级640名学生在“计算机应用”培训前、后各参加了一次水平相同的测试,并以同一标准分成“不合格”、“合格”、“优秀”3个等级,为了解培训效果,用抽样调查的方式从中抽取32名学生的2次测试等级,并绘制成条形统计图:

(1)这32名学生经过培训,测试等级“不合格”的百分比比培训前减少了多少?
(2)估计该校八年级学生中,培训前、后等级为“合格”与“优秀”的学生各有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com