
 如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )
如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
分析 顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.
解答  解:如图,连接AC,
解:如图,连接AC,
∵E、F、G、H分别是四边形ABCD边的中点,
∴HG∥AC,HG=$\frac{1}{2}$AC,EF∥AC,EF=$\frac{1}{2}$AC;
∴EF=HG且EF∥HG;
∴四边形EFGH是平行四边形.
故选:A.
点评 此题主要考查了平行四边形的判定以及三角形的中位线定理,根据已知利用三角形中位线定理得出EH∥BD,EH=$\frac{1}{2}$BD,FG∥BD,FG=$\frac{1}{2}$BD是解决问题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.
如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连结ED,EC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )| A. | ${(\frac{1}{2})}^{2015}$ | B. | ${(\frac{1}{2})}^{2016}$ | C. | ${(\frac{\sqrt{3}}{3})}^{2015}$ | D. | ${(\frac{\sqrt{3}}{3})}^{2016}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{41}$ | B. | $\sqrt{52}$ | C. | $\sqrt{26}$ | D. | $\root{3}{38}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
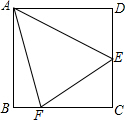 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 420 | B. | 434 | C. | 450 | D. | 465 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com