
【题目】在同一坐标系中,二次函数![]() 与一次函数
与一次函数![]() 的图像可能是( )
的图像可能是( )
A.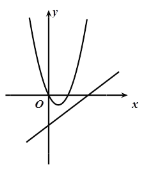 B.
B.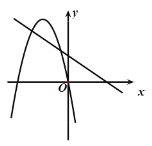
C.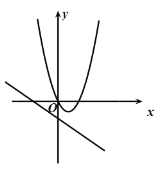 D.
D.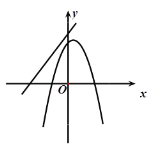
【答案】C
【解析】
直线与抛物线联立解方程组,若有解,则图象有交点,若无解,则图象无交点;
根据二次函数的对称轴在y左侧,a,b同号,对称轴在y轴右侧a,b异号,以及当a大于0时开口向上,当a小于0时开口向下,来分析二次函数;同时在假定二次函数图象正确的前提下,根据一次函数的一次项系数为正,图象从左向右逐渐上升,一次项系数为负,图象从左向右逐渐下降;一次函数的常数项为正,交y轴于正半轴,常数项为负,交y轴于负半轴.如此分析下来,二次函数与一次函数无矛盾者为正确答案.
解:由方程组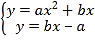 得ax2=a,
得ax2=a,
∵a≠0
∴x2=1,该方程无实数根,
故二次函数与一次函数图象无交点,排除B.
A:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;但是一次函数b为一次项系数,图象显示从左向右上升,b>0,两者矛盾,故A错;
C:二次函数开口向上,说明a>0,对称轴在y轴右侧,则b<0;b为一次函数的一次项系数,图象显示从左向右下降,b<0,两者相符,故C正确;
D:二次函数的图象应过原点,此选项不符,故D错.
故选C.


科目:初中数学 来源: 题型:
【题目】设一次函数y=ax+b(a,b是常数,且a≠0)的图象A(1,3)和B(-1,-1)两点.
(1)求该一次函数的表达式.
(2)①若点(![]() ,2)在(1)中的函数图象上,求m的值.
,2)在(1)中的函数图象上,求m的值.
②若(1)中的函数图象和y=-2x+n的函数图象的交点在第一象限,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标分别是
的坐标分别是![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 在第一、二象限的抛物线上,过点
在第一、二象限的抛物线上,过点![]() 作
作![]() 轴的平行线分别交
轴的平行线分别交![]() 轴和直线
轴和直线![]() 于点
于点![]() 、
、![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长度为
的长度为![]() .
.
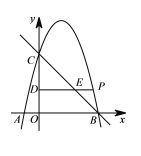
⑴求这条抛物线对应的函数表达式;
⑵当点![]() 在第一象限的抛物线上时,求
在第一象限的抛物线上时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
⑶在⑵的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变世界.随着科技的发展,自动化程度越来越高,机器人市场越来越火.某商场购进一批![]() ,
,![]() 两种品牌的编程机器人,进价分别为每台3000元、4000元.市场调查发现:销售3个
两种品牌的编程机器人,进价分别为每台3000元、4000元.市场调查发现:销售3个![]() 品牌机器人和2个
品牌机器人和2个![]() 品牌机器人,可获利润6000元;销售2个
品牌机器人,可获利润6000元;销售2个![]() 品牌机器人和3个
品牌机器人和3个![]() 品牌机器人,可获利润6500元.
品牌机器人,可获利润6500元.
(1)此商场![]() .
.![]() 两种品牌的编程机器人销售价格分别是多少元?
两种品牌的编程机器人销售价格分别是多少元?
(2)若商场准备用不多于65000元的资金购进![]() ,
,![]() 两种品牌的编程机器人共20个,则至少需要购进
两种品牌的编程机器人共20个,则至少需要购进![]() 品牌的编程机器人多少个?
品牌的编程机器人多少个?
(3)不考虑其它因素,商场打算![]() 品牌编程机器人数量不多于
品牌编程机器人数量不多于![]() 品牌编程机器人数量的
品牌编程机器人数量的![]() ,现打算购进
,现打算购进![]() ,
,![]() 两种品牌编程机器人共40个,怎样进货才能获得最大的利润?
两种品牌编程机器人共40个,怎样进货才能获得最大的利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生假期主题阅读的情况(要求每名学生的文章阅读篇数,最少3篇,最多7篇),随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 20 | 28 |
| 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生读书总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
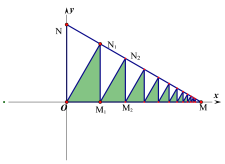
【题目】在平面直角坐标系中,直线![]() 与两坐标轴分别交于M、N两点,过点O作
与两坐标轴分别交于M、N两点,过点O作![]() ,过
,过![]() 作
作![]() ,得阴影
,得阴影![]() ;再过
;再过![]() 作
作![]() ,过
,过![]() 作
作![]() ,得阴影
,得阴影![]() ;……如此进行下去,则得到的所有阴影三角形的面积之和为_________.
;……如此进行下去,则得到的所有阴影三角形的面积之和为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
⑴求v关于t的函数表达式;
⑵方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com