
【题目】如图,![]() 是
是![]() 的中线,
的中线,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 延长线上的点,且
延长线上的点,且![]() ,连接
,连接![]() 、
、![]() ,下列说法:①
,下列说法:①![]() 和
和![]() 的面积相等,②
的面积相等,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中一定正确的答案有______________.(只填写正确的序号)
,其中一定正确的答案有______________.(只填写正确的序号)
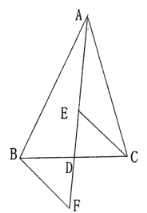
【答案】①③④⑤
【解析】
根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确;利用“SAS”证明③△BDF≌△CDE正确,根据全等三角形对应边相等,证明⑤正确,根据全等三角形对应角相等得∠F=∠DEF,再根据内错角相等,两直线平行可得④正确.
解:由题意得 BD=CD,点A到BD,CD的距离相等
∴△ABD和△ACD的面积相等,故①正确;
虽然已知AD为△ABC的中线,但是推不出来∠BAD和∠CAD一定相等,故②不正确;
在△BDF和△CDE中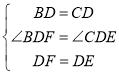 ,
,
∴△BDF≌△CDE,故③正确;
∴CE=BF,故⑤正确;
∴∠F=∠DEF
∴BF∥CE,故④正确;
故答案为①③④⑤.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
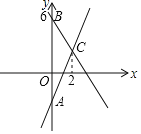
【题目】如图,一次函数y1=2x﹣2的图象与y轴交于点A,一次函数y2的图象与y轴交于点B(0,6),点C为两函数图象交点,且点C的横坐标为2.
(1)求一次函数y2的函数解析式;
(2)求△ABC的面积;
(3)问:在坐标轴上,是否存在一点P,使得S△ACP=2S△ABC,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
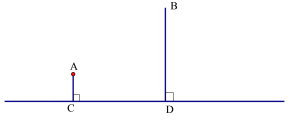
(1)现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
方案1:水厂建在C点,修自来水管道到A村,再到B 村(即AC+AB).(如图)
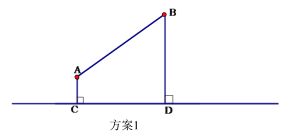
方案2:作A点关于直线CD的对称点![]() ,连接
,连接![]() 交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
交CD 于M点,水厂建在M点处,分别向两村修管道AM和BM. (即AM+BM) (如图)
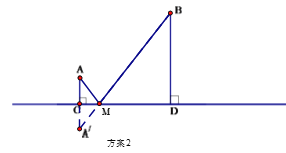
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算,判断哪种方案更合适.
(2)有一艘快艇Q从这条河中驶过,当快艇Q与CD中点G相距多远时,△ABQ为等腰三角形?直接写出答案,不要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() .设
.设![]() 为最长边.当
为最长边.当![]() 时,
时,![]() 是直角三角形;当
是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,探究
的大小关系,探究![]() 的形状(按角分类).
的形状(按角分类).
(1)当![]() 三边分别为6、8、9时,
三边分别为6、8、9时,![]() 为______三角形;当
为______三角形;当![]() 三边分别为6、8、11时,
三边分别为6、8、11时,![]() 为______三角形.
为______三角形.
(2)猜想,当![]() ______
______![]() 时,
时,![]() 为锐角三角形;当
为锐角三角形;当![]() ______
______![]() 时,
时,![]() 为钝角三角形.
为钝角三角形.
(3)判断当![]() ,
,![]() 时,
时,![]() 的形状,并求出对应的
的形状,并求出对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
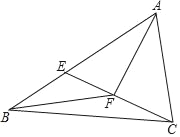
【题目】△ABC中,AB=CB,AC=10,S△ABC=60,E为AB上一动点,连结CE,过A作AF⊥CE于F,连结BF,则BF的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
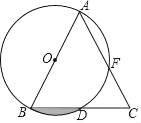
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC交⊙O于点F.
(1)AB与AC的大小有什么关系?请说明理由;
(2)若AB=8,∠BAC=45°,求:图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用![]() 元购进某种干果销售,由于销售状况良好,超市又调拨
元购进某种干果销售,由于销售状况良好,超市又调拨![]() 元资金购进该种干果,但这次的进价比第一次的进价提高了
元资金购进该种干果,但这次的进价比第一次的进价提高了![]() ,购进干果数量是第一次的
,购进干果数量是第一次的![]() 倍还多
倍还多![]() 千克.
千克.
![]() 该种干果的第一次进价是每千克多少元?
该种干果的第一次进价是每千克多少元?
![]() 如果超市将这种干果全部按每千克
如果超市将这种干果全部按每千克![]() 元的价格出售,售完这种干果共盈利多少元?
元的价格出售,售完这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在反比例函数y=![]() 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
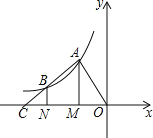
A.2 B.4 C.﹣2 D.﹣4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com