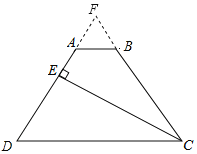
【题目】在梯形ABCD中，AB∥CD，CE平分∠BCD，CE⊥AD于E，DE＝2AE．若△CED面积为1，则四边形ABCE的面积为（ ）
A.
B.
C.
D.
【答案】B
【解析】
延长DA、CB相交于点F，证出∠D=∠F，得出CD=CF，DE=FE，求出AE=AF=
DE，得出
，△CFE的面积=△CDE的面积=1，△FDC的面积=2△CDE的面积=2，证明△FAB∽△FDC，得出S△FAB=
，即可得出答案．
解：如图，延长DA、CB相交于点F，
∵CE平分∠BCD，CE⊥AD，
∴∠D＝∠F，
∴CD＝CF，DE＝FE，
∴△CFE的面积＝△CDE的面积＝1，
∴△FDC的面积＝2△CDE的面积＝2，
∵DE＝2AE，
∴AE＝AF＝DE，
∴，
∵AB∥CD，
∴△FAB∽△FDC，
∴S△FAB＝
S△FDC＝×2＝
，
∴四边形ABCE的面积＝1﹣＝
；
故选：B．
科目：初中数学 来源： 题型：
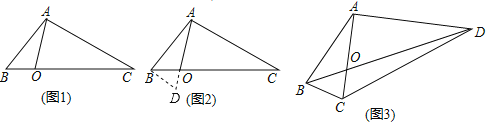
【题目】（1）某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=
，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= °，AB= ．
（2）请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
的图象过点
、顶点
的横坐标为.
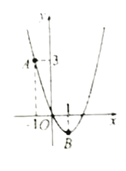
（1）求这个二次函数的解析式；
（2）点
在该一次函数的图象上，点
在
轴上，若以
为顶点的四边形是平行四边形，求点的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】元旦期间，某宾馆有50个房间供游客居住，当每个房间每天的定价为180元时，房间会全部住满；当每个房间每天的定价每增加10元时，就会有一个房间空闲．如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用．
（1）若房价定为200元时，求宾馆每天的利润；
（2）房价定为多少时，宾馆每天的利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，点D是△ABC中BC边上的中点，DE⊥AC，DF⊥AB，垂足分别是点EF，且BF＝CE．
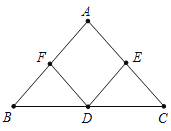
（1）求证：Rt△BDF≌Rt△CDE
（2）问：△ABC满足什么条件时，四边形AEDF是正方形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，AC交DE于点F．
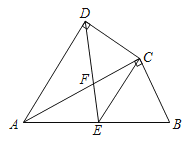
（1）求证：AC2＝ABAD；
（2）求证：CE∥AD；
（3）若AD＝5，AB＝6，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
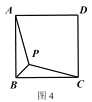
【题目】(1) 知识储备
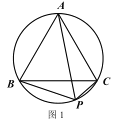
①如图 1，已知点 P 为等边△ABC 外接圆的弧BC 上任意一点．求证：PB+PC= PA.
②定义：在△ABC 所在平面上存在一点 P，使它到三角形三顶点的距离之和最小，则称点 P 为△ABC
的费马点，此时 PA+PB+PC 的值为△ABC 的费马距离．
(2)知识迁移
①我们有如下探寻△ABC (其中∠A，∠B，∠C 均小于 120°)的费马点和费马距离的方法：
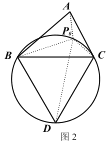
如图 2，在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆，根据(1)的结论，易知线段____的长度即为△ABC 的费马距离.
②在图 3 中，用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题（正确的打√，错误的打×）：
ⅰ.任意三角形的费马点有且只有一个（__________）；
ⅱ.任意三角形的费马点一定在三角形的内部（__________）.
②已知正方形 ABCD，P 是正方形内部一点，且 PA+PB+PC 的最小值为
，求正方形 ABCD 的
边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数(单位：元)，并绘制成下面的统计图．
(1)本次调查的样本容量是 ，这组数据的众数为 元；中位数为 元；
(2)求这组数据的平均数；
(3)该校共有600名学生参与捐款，请你估计该校学生的捐款总数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
