

���� ��1�����ۣ�BE=DF��ֻҪ֤����AEB�ա�AFD���ɣ�
��2�����ۣ�CE-FD=BD���ɡ�AEB�ա�AFD����BE=DF���ɴ˼���֤����
��3�����ۣ�90��-����ֻҪ֤����AOB=��AOF=90�㼴�ɽ�����⣮
��� �⣺��1�����ۣ�BE=DF��
���ɣ���ͼ1�У�
�ߵ�����ABC�͡�ABDȫ�ȣ�
��AB=AC=AD����C=��ABC=��ABD=��D����BAC=��BAD��
�ߡ�MAN=��BAC=����
���MAN=��BAD=����
���EAB=��FAD��
�ڡ�AEB�͡�AFD�У�
$\left\{\begin{array}{l}{��ABE=��D}\\{AB=AD}\\{��EAB=��FAD}\end{array}\right.$��
���AEB�ա�AFD��
��BE=DF��
��2�����ۣ�CE-FD=BD��
���ɣ���ͼ2����ʾ���ߡ�MAN=��BAD��
���DAF=��BAE��
�ߡ�ABC=��ADB��
���ABE=��ADF��
�ڡ�ABE�͡�ADF�У�
$\left\{\begin{array}{l}{��ABE=��ADF}\\{AB=AD}\\{��BAE=��DAF}\end{array}\right.$��
���AEB�ա�AFD��
��BE=DF��
��BC=BD��
��CE-FD=CE-BE=BC=BD��
��3�����ۣ�90��-����
���ɣ���ͼ3�У�AE��BD�ڵ�O��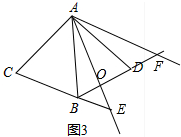
��AD��EF��
���DAF+��AFE=90�㣬
�ߡ�DAF=��BAE����ABD=��AFE��
���OAB+��OBA=90�㣬
���AOB=��AOF=90�㣬
���AFD=90��-��EAF=90��-����
�ߡ�CEA=��AFD��
���CEA=90��-����
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʣ�����Ĺؼ�����������ȫ�������ε��ж������ʣ���ȷѰ��ȫ�������Σ������п��������ͣ�


 �������Ͽ��㱾ϵ�д�
�������Ͽ��㱾ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3cm��8cm��7cm | B�� | 4cm��5cm��6cm | C�� | 6cm��8cm��15cm | D�� | 8cm��9cm��15cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\sqrt{3}$ | C�� | -2 | D�� | ��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
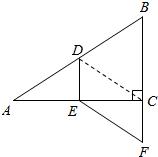 ��ͼ����Rt��ABC�У���ACB=90�㣬��D��E�ֱ��DZ�AB��AC���е㣬�ӳ�BC��F��ʹCF=$\frac{1}{2}$BC����AB=10����EF�ij��ǣ�������
��ͼ����Rt��ABC�У���ACB=90�㣬��D��E�ֱ��DZ�AB��AC���е㣬�ӳ�BC��F��ʹCF=$\frac{1}{2}$BC����AB=10����EF�ij��ǣ�������| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com