
(2013年四川泸州10分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
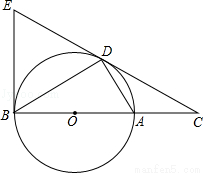
(1)求证:CD2=CA•CB;
(2)求证:CD是⊙O的切线;
(3)过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA=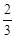 ,求BE的长.
,求BE的长.
解:(1)证明:∵∠CDA=∠CBD,∠C=∠C,
∴△ADC∽△DBC,
∴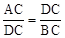 ,即CD2=CA•CB。
,即CD2=CA•CB。
(2)证明:如图,连接OD,
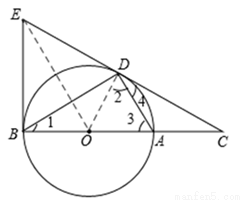
∵AB是⊙O的直径,∴∠ADB=90°。∴∠1+∠3=90°。
∵OA=OD,∴∠2=∠3。∴∠1+∠2=90°。
又∵∠CDA=∠CBD,即∠4=∠1,
∴∠4+∠2=90°,即∠CDO=90°。∴OD⊥OA。
又∵OA是⊙O的半径,∴CD是⊙O的切线。
(3)如图,连接OE,
∵EB、CD均为⊙O的切线,∴ED=EB,OE⊥DB。
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°。∴∠ABD=∠OEB。∴∠CDA=∠OEB。
∵tan∠CDA= ,∴
,∴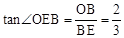 。
。
∵Rt△CDO∽Rt△CBE,∴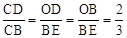 。
。
∵BC=12,∴CD=8。
在Rt△CBE中,设BE=x,
∴(x+8)2=x2+122,解得x=5。
∴BE的长为5。
【解析】(1)通过相似三角形(△ADC∽△DBC)的对应边成比例来证得结论。
(2)如图,连接OD.欲证明CD是⊙O的切线,只需证明CD⊥OA即可。
(3)通过相似三角形△EBC∽△ODC的对应边成比例列出关于BE的方程,通过解方程来求线段BE的长度即可。
考点:切线的判定和性质,相似三角形的判定和性质,圆周角定理,勾股定理。


科目:初中数学 来源:2013年初中毕业升学考试(四川泸州卷)数学(解析版) 题型:解答题
(2013年四川泸州8分)如图,已知函数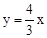 与反比例函数
与反比例函数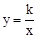 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将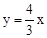 的图象向下平移6个单位后与双曲线
的图象向下平移6个单位后与双曲线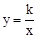 交于点B,与x轴交于点C.
交于点B,与x轴交于点C.
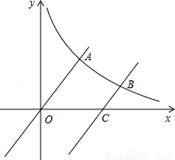
(1)求点C的坐标;
(2)若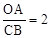 ,求反比例函数的解析式.
,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川泸州卷)数学(解析版) 题型:解答题
(2013年四川泸州8分)如图,为了测出某塔CD的高度,在塔前的平地上选择一点A,用测角仪测得塔顶D的仰角为30°,在A、C之间选择一点B(A、B、C三点在同一直线上).用测角仪测得塔顶D的仰角为75°,且AB间的距离为40m.

(1)求点B到AD的距离;
(2)求塔高CD(结果用根号表示).
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川泸州卷)数学(解析版) 题型:解答题
(2013年四川泸州7分)某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川泸州卷)数学(解析版) 题型:解答题
(2013年四川泸州7分)某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画.要求每位同学必须参加,且限报一项活动.以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图.请你结合图示所给出的信息解答下列问题.
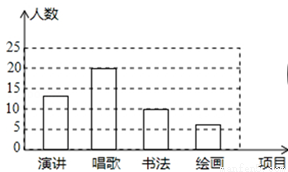
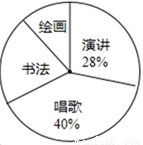
(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com