
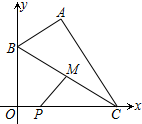
 在平面直角坐标系中,已知A(2,4)、P(1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°.M为BC的中点,则PM的最小值为$\frac{4\sqrt{5}}{5}$.
在平面直角坐标系中,已知A(2,4)、P(1,0),B为y轴上的动点,以AB为边构造△ABC,使点C在x轴上,∠BAC=90°.M为BC的中点,则PM的最小值为$\frac{4\sqrt{5}}{5}$. 分析 如图,作AH⊥y轴于H,CE⊥AH于E.则四边形CEHO是矩形,OH=CE=4,由△AHB∽△CEA,得$\frac{AH}{EC}$=$\frac{BH}{AE}$,推出$\frac{2}{4}$=$\frac{BH}{AE}$,推出AE=2BH,设BH=x则AE=2x,推出B(0,4-x),C(2+2x,0),由BM=CM,推出M(1+x,$\frac{4-x}{2}$),可得PM=$\sqrt{{x}^{2}+(\frac{4-x}{2})^{2}}$=$\sqrt{\frac{5}{4}(x-\frac{4}{5})^{2}+\frac{16}{5}}$,由此即可解决问题.
解答 解:如图,作AH⊥y轴于H,CE⊥AH于E.则四边形CEHO是矩形,OH=CE=4,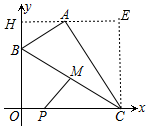
∵∠BAC=∠AHB=∠AEC=90°,
∴∠ABH+∠HAB=90°,∠HAB+∠EAC=90°,
∴∠ABH=∠EAC,
∴△AHB∽△CEA,
∴$\frac{AH}{EC}$=$\frac{BH}{AE}$,
∴$\frac{2}{4}$=$\frac{BH}{AE}$,
∴AE=2BH,设BH=x则AE=2x,
∴OC=HE=2+2x,OB=4-x,
∴B(0,4-x),C(2+2x,0)
∵BM=CM,
∴M(1+x,$\frac{4-x}{2}$),∵P(1,0),
∴PM=$\sqrt{{x}^{2}+(\frac{4-x}{2})^{2}}$=$\sqrt{\frac{5}{4}(x-\frac{4}{5})^{2}+\frac{16}{5}}$,
∴x=$\frac{4}{5}$时,PM有最小值,最小值为$\frac{4\sqrt{5}}{5}$.
故答案为$\frac{4\sqrt{5}}{5}$.
点评 本题考查相似三角形的判定和性质、两点间距离公式、二次函数的应用等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,学会构建二次函数,利用二次函数的性质解决最值问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | (1,3) | B. | (3,1) | C. | (2,1) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
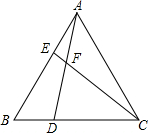 如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.
如图,在△ABC中,∠BAC=∠B=60°,点D、E分别是边BC、AB所在直线上的动点,且BD=AE,AD与CE交于点F,当点D、E在边BC、AB上运动时,∠DFC的度数是否发生变化?若不变,求出其度数;若变化,写出其变化规律.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同旁内角互补 | |
| B. | 一个角的补角大于这个角 | |
| C. | 同位角不相等,两直线不平行 | |
| D. | 如果两个角不相等,那么这两个角不是对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.
如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com