
分析 把$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$代入4x-by=-2求出b,把$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$代入ax+5y=15求出a,代入求出即可.
解答 解:根据题意把$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$代入4x-by=-2得:-12+b=-2,
解得:b=10,
把$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$代入ax+5y=15得:5a+20=15,
解得:a=-1,
所以a2015+(-$\frac{1}{10}$b)2016=(-1)2015+(-$\frac{1}{10}$×10)2016=0.
点评 本题考查了二元一次方程组的解,解一元一次方程,求代数式的值的应用,能求出a、b的值是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
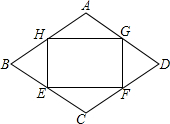 如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.
如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
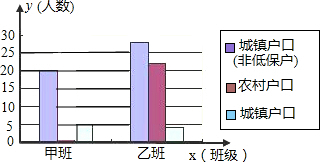
类型 班级 | 城镇户口 (非低保) | 农村 户口 | 城镇 低保 | 总人数 |
| 甲班/人 | 20 | 25 | 5 | 50 |
| 乙班/人 | 28 | 22 | 4 | 54 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com