
【题目】已知A(1,5),B(3,-1)两点,在x轴上取一点M,使AM-BM取得最大值时,则M的坐标为 ▲
【答案】(![]() ,0).
,0).
【解析】
一次函数综合题,线段中垂线的性质,三角形三边关系,关于x轴对称的点的坐标,待定系数法,直线上点的坐标与方程的关系,解二元一次方程组.
此时AM-BM=AM-B′M=AB′.

不妨在x轴上任取一个另一点M′,连接M′A、M′B、M′B.
则M′A-M′B=M′A-M′B′<AB′(三角形两边之差小于第三边).
∴M′A-M′B<AM-BM,即此时AM-BM最大.
∵B′是B(3,-1)关于x轴的对称点,∴B′(3,1).
设直线AB′解析式为y=kx+b,把A(1,5)和B′(3,1)代入得:
![]() ,解得
,解得![]() .∴直线AB′解析式为y=-2x+7.
.∴直线AB′解析式为y=-2x+7.
令y=0,解得x=![]() .∴M点坐标为(
.∴M点坐标为(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知一抛物线的顶点![]() 的坐标是
的坐标是![]() ,并且抛物线与
,并且抛物线与![]() 轴两交点间的距离为
轴两交点间的距离为![]() .
.
![]() 试求该抛物线的关系式;
试求该抛物线的关系式;
![]() 若点
若点![]() 在此抛物线上,且点
在此抛物线上,且点![]() 在第一象限,求以点
在第一象限,求以点![]() 、
、![]() 和坐标原点
和坐标原点![]() 为顶点的
为顶点的![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABC=90°, P为射线BC上任意一点(点P和点B不重合),分别以AB,AP为边在∠ABC内部作等边△ABE和等边△APQ, 连结QE并延长交BP于点F, 若FQ=6, AB=2![]() ,则BP=__________
,则BP=__________
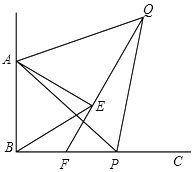
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售A B两种型号的电风扇,A型号每台进价为200元,B型号每台进价分别为150元,下表是近两天的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一天 | 3台 | 5台 | 1620元 |
第二天 | 4台 | 10台 | 2760元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润不少于1060元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内有两点P1 x1,y1 ,P1 x2,y2 其两点间的距离P1P2 = ![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2 x1|或|y2 y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2 x1|或|y2 y1|.
(1)已知 A (1,4)、B (-3,5),试求 A.、B两点间的距离;
(2)已知 A、B在平行于 y轴的直线上,点 A的纵坐标为-8,点 B的纵坐标为-1,试求 A、B两点的距 离;
(3)已知一个三角形各顶点坐标为 D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由:
(4)在(3)的条件下,平面直角坐标系中,在 x轴上找一点 P,使 PD+PF的长度最短,求出点 P的坐 标以及 PD+PF的最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017怀化,第10题,4分)如图,A,B两点在反比例函数![]() 的图象上,C,D两点在反比例函数
的图象上,C,D两点在反比例函数![]() 的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则
的图象上,AC⊥y轴于点E,BD⊥y轴于点F,AC=2,BD=1,EF=3,则![]() 的值是( )
的值是( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点 B、O分别落在点 B1、C1 处,点B1在x轴上,再将△AB1C1 绕点 B1 顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2 绕点C2 顺时针旋转到△A2B2C2 的位置,点 A2 在x轴上,依次进行下去….若点 A(![]() ,0),B(0,4),则点 B2016 的横坐标为_______.
,0),B(0,4),则点 B2016 的横坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BD是∠ABC的平分线,AD⊥BD,垂足是D.
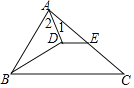
(1)求证:∠2=∠1+∠C;
(2)若ED∥BC,∠ABD=28°,求∠ADE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com