
【题目】如图,四边形ABCD是⊙O的内接四边形,且AC⊥BD,OF⊥AB,垂足分别为E、F,请问OF与CD有怎样的数量关系?

【答案】OF=![]() CD.理由见解析.
CD.理由见解析.
【解析】试题分析:连接AO并延长,与⊙O相交于点G,连接BG,根据同弧所对的圆周角相等可得∠G=∠ADB,再根据等角的余角相等求出∠DAE=∠BAG,然后根据相等的圆周角所对的弦相等可得CD=BG,根据垂径定理可得AF=BF,从而得到OF是△ABG的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半可得OF=![]() BG.
BG.
试题解析:OF=![]() CD.
CD.
理由如下:如图,连接AO并延长,与⊙O相交于点G,连接BG,
则∠G=∠ADB,
∵AC⊥BD,
∴∠DAE+∠ADB=90°,
∵AG是直径,
∴∠BAG+∠G=90°,
∴∠DAE=∠BAG,
∴CD=BG,
∵OF⊥AB,
∴AF=BF,
∴OF是△ABG的中位线,
∴OF=![]() BG,
BG,
故OF=![]() CD.
CD.



科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④
图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④ ![]() <0.其中正确结论的个数是( )
<0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:材料1 若一元二次方程![]() 的两根为
的两根为![]() 、
、![]() ,则
,则![]() ,
, ![]()
材料2:已知实数![]() 、
、![]() 满足
满足![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
解:由题知![]() 、
、![]() 是方程
是方程![]() 的两个不相等的实数根,根据材料1得
的两个不相等的实数根,根据材料1得![]() ,
, ![]()
![]()
根据上述材料解决下面问题:
(1)一元二次方程![]() 的两根为
的两根为![]() 、
、![]() ,则
,则![]() = ,
= , ![]() = 。
= 。
(2)已知实数![]() 、
、![]() 满足
满足![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)已知实数![]() 、
、![]() 满足
满足![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为( )
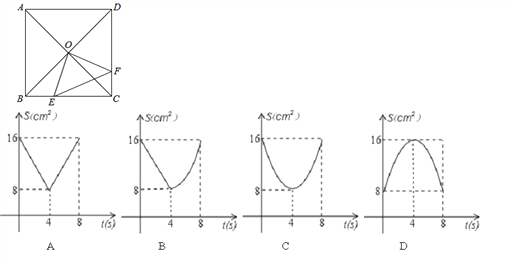
A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D, AC交⊙O于点E,∠BAC=45°。
(1)求∠EBC的度数;
(2)求证:BD=CD。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于函数![]() 的四个命题:①当
的四个命题:①当![]() 时,
时, ![]() 有最小值10;②
有最小值10;②![]() 为任意实数,
为任意实数, ![]() 时的函数值大于
时的函数值大于![]() 时的函数值;③若
时的函数值;③若![]() ,且
,且![]() 是整数,当
是整数,当![]() 时,
时, ![]() 的整数值有
的整数值有![]() 个;④若函数图象过点
个;④若函数图象过点![]() 和
和![]() ,其中
,其中![]() ,
, ![]() ,则
,则![]() .其中真命题的序号是( )
.其中真命题的序号是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解本校学生周末玩手机所花时间的情况,七、八、九年级中各抽取50名学生(男女各25名)进行调查,此次调查所抽取的样本容量是( )
A. 150B. 75C. 50D. 25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com