
分析 根据题意画出图形,分类讨论,利用三角形的内角和定理和等腰三角形的性质可得结论.
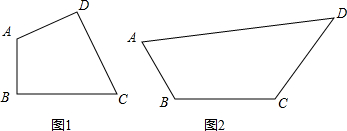
解答 解:①当BD=CD,CD=AD时,如图①所示,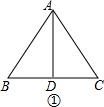 ∵AB=AC,
∵AB=AC,
∴∠B=∠C,
设∠B=∠C=x,
∵BD=CD,CD=AD,
∴∠BAD=∠B=x,∠CAD=∠C=x,
∴4x=180°,
∴x=45°,
∴∠BAC=2x=45°×2=90°;
②当AD=BD,AC=CD时,如图②所示,
∵ AB=AC,
AB=AC,
∴∠B=∠C
设∠B=∠C=x,
∵AD=BD,AC=CD,
∴∠BAD=∠B=x,∠CAD=$\frac{180°-x}{2}$,
∴$\frac{180°-x}{2}+x$=180°-2x,
解得:x=36°,
∴∠BAC=180°-2x=180°-2×36°=108°,
故答案为:90°或108°.
点评 本题主要考查了等腰三角形的性质,根据题意画出图形分类讨论,利用三角形的内角和定理是解答此题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
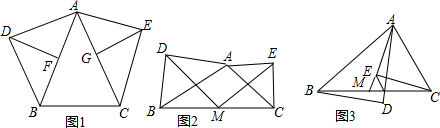
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
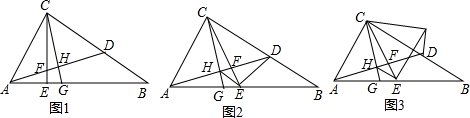
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 12 | C. | 12或16 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:
如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,连接EF交AP于点G,给出以下五个结论:| A. | 只有① | B. | ①②④ | C. | ①②③④ | D. | ①②④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
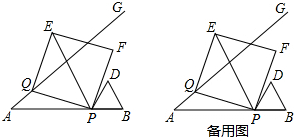
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com