
分析 由矩形的性质得出OC=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,得出OB=OC,得出∠OBC=∠OCB,求出∠OBC=∠OCB=62°,即可得出∠OCH的度数.
解答 解:如图所示:
∵四边形ABCD是矩形,
∴OC=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
∵CH⊥BD,
∴∠CHB=90°,
∴∠OBC=90°-28°=62°,
∴∠OCB=62°,
∴∠OCH=∠OCB-∠BCH=62°-28°=34°.
点评 本题考查了矩形的性质、等腰三角形的性质、角的互余关系;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:解答题
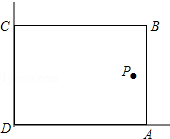 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x(m).
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x(m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com