
已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.
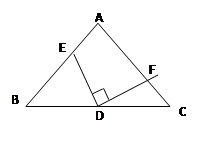
1.如果∠A=90°求证:DE=DF
2.如果DF//AB,则结论:“四边形AEDF为直角梯形”是否正确,若正确,请证明;若不正确,请画出草图举反例
1.连接AD
∵AB=AC,D是BC的中点,∠A=90°
∴AD=DC, ∠BAD=∠C,
∵∠ADC=90°, ∠EDF=90°
∴∠EDA=∠FDC
∴△ADE≌△CDF 得到DE=DF………………………………4分
2.结论不正确. 图略 ………………………………1分
反例如下:
取![]() 时,四边形ADEF为矩形,不是直角梯形。
时,四边形ADEF为矩形,不是直角梯形。
![]() DF//AB,
DF//AB, ![]()
∴∠AED=90°
当![]() 时,四边形ADEF为矩形,不是直角梯形。
时,四边形ADEF为矩形,不是直角梯形。
∴结论不正确………………………………4分
解析:(1)根据等腰直角三角形的性质得到∠C=45°,中线AD平分∠BAC,并且AD=![]() BC,则∠BAD=∠C,AD=DC,又∠EDA=∠CDF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
BC,则∠BAD=∠C,AD=DC,又∠EDA=∠CDF,根据全等三角形的判定易得到△ADE≌△CDF,然后根据全等三角形的性质即可得到结论.
(2)举出反例。


科目:初中数学 来源: 题型:
 24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;
24、(1)如图,△ABC纸片中,∠A=36°,AB=AC,请你剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形.请画出示意图,并标明必要的角度;查看答案和解析>>
科目:初中数学 来源: 题型:
| 120 |
| 13 |
| 120 |
| 13 |

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com