
【题目】如图,已知一次函数y=2x的图象与反比例函数y=![]() (x>0),y=
(x>0),y=![]() (x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=
(x>0)的图象分别交于P,Q两点,点P为OQ的中点,Rt△ABC的直角顶点A是双曲线y=![]() (x>0)上一动点,顶点B,C在双曲线y=
(x>0)上一动点,顶点B,C在双曲线y=![]() (x>0)上,且两直角边均与坐标轴平行.
(x>0)上,且两直角边均与坐标轴平行.
(1)直接写出k的值;
(2)△ABC的面积是否变化?若不变,求出△ABC的面积;若变化,请说明理由;
(3)直线y=2x是否存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,若存在,求出点A的坐标;若不存在,请说明理由.

【答案】(1)8;(2)△ABC的面积不变,![]() ;(3)存在,(
;(3)存在,(![]() ,
,![]() )、(
)、(![]() ,
,![]() )或(2,4).
)或(2,4).
【解析】
(1)设点P(m,![]() ),Q(n,
),Q(n,![]() ),根据P为OQ的中点,即可得出m、n之间的关系,由此即可得出k值;
),根据P为OQ的中点,即可得出m、n之间的关系,由此即可得出k值;
(2)△ABC的面积不变,设A(a,![]() )(a>0),根据AB、AC与坐标轴平行找出点B、C的坐标,由此即可得出AB、AC,再根据三角形的面积公式即可得出结论;
)(a>0),根据AB、AC与坐标轴平行找出点B、C的坐标,由此即可得出AB、AC,再根据三角形的面积公式即可得出结论;
(3)假设存在,设A(a,![]() )(a>0),则C(a,
)(a>0),则C(a,![]() ),B(
),B(![]() ,
,![]() ).以A,B,C,D为顶点的四边形分别是以AB、AC、BC为对角线的平行四边形,根据平行四边形对角线互相平分的性质找出点D的坐标,再根据点D在直线y=2x上找出关于a的方程,解方程求出a值,将其代入A点坐标中即可得出结论.
).以A,B,C,D为顶点的四边形分别是以AB、AC、BC为对角线的平行四边形,根据平行四边形对角线互相平分的性质找出点D的坐标,再根据点D在直线y=2x上找出关于a的方程,解方程求出a值,将其代入A点坐标中即可得出结论.
解:(1)∵点P在反比例函数y=![]() (x>0)上,点Q在反比例函数y=
(x>0)上,点Q在反比例函数y=![]() (x>0)上,
(x>0)上,
∴设点P(m,![]() ),Q(n,
),Q(n,![]() ),
),
∵点P为OQ的中点,
∴n=2m,![]() =2
=2![]() ,
,
∴k=8.
(2)△ABC的面积不变,
设A![]()
![]() ,则C
,则C![]() ,
,
令y=![]() 中y=
中y=![]() ,则x=
,则x=![]() ,
,
∴点B(![]() ,
,![]() ),
),
∴AB=![]() =
=![]() ,AC=
,AC=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△ABC=![]() ABAC=
ABAC=![]()
![]() =
=![]() .
.
(3)假设存在,设A![]()
![]() ,则C
,则C![]() ,B(
,B(![]() ,
,![]() ).
).
以A,B,C,D为顶点的四边形是平行四边形分三种情况:
①以AB为对角线,
则点D(![]() ,
,![]() ),即(
),即(![]() ,
,![]() ),
),
∵点span>D在y=2x上,
∴![]() =2
=2![]() ,
,
解得:a=![]() 或a=
或a=![]() (舍去),
(舍去),
此时点A(![]() ,
,![]() );
);
②以AC为对角线,
则点D(![]() ,
,![]() ),即(
),即(![]() ,
,![]() ),
),
∵点D在y=2x上,
∴![]() =2
=2![]() ,
,
解得:a=![]() 或a=﹣
或a=﹣![]() (舍去),
(舍去),
此时点A(![]() ,
,![]() );
);
③以BC为对角线,
则点D(![]() ,
,![]() ),即(
),即(![]() ,
,![]() ),
),
∵点D在y=2x上,
∴![]() =2
=2![]() ,
,
解得:a=2或a=﹣2(舍去),
此时点A(2,4).
故直线y=2x存在点D,使得以A,B,C,D为顶点的四边形是平行四边形,点A的坐标为(![]() ,
,![]() )、(
)、(![]() ,
,![]() )或(2,4).
)或(2,4).


科目:初中数学 来源: 题型:
【题目】阅读并解决问题:归纳
人们通过长期观察发现,如果早晨天空中有棉絮状的高积云,那么午后常有雷雨降临,于是有了“朝有破絮云,午后雷雨临”的谚语.在数学里,我们也常用这样的方法探求规律,例如:三角形有3个顶点,如果在它的内部再画n个点,并以(n+3)个点为顶点,把三角形剪成若干个小三角形,那么最多可以剪得多少个这样的三角形? .为了解决这个问题,我们可以从n=1、n=2、nr=3 等具体的、简单的情形入手,探索最多可以剪得的三角形个数的变化规律.

(1)完成表格信息:_______、_________;
(2)通过观察、比较,可以发现:三角形内的点每增加1个,最多可以剪得的三角形增加_________个.于是,我们可以猜想:当三角形内的点的个数为n时,最多可以剪得____________个三角形.像这样通过对现象的观察、分析,从特殊到-般地探索这类现象的规律、提出猜想的思想方法称为归纳.在日常生活中,人们互相交谈时,常常有人在列举了一些现象后,说“这(即列举的现象)说明....其实这就是运用了归纳的方法.用归纳的方法得出的结论不一定正确,是否正确需要加以证实.
(3)请你借助表格尝试用归纳的方法探索: 1+3+5+7+......+(2n-1)的和是多少?并加以证实.
查看答案和解析>>
科目:初中数学 来源: 题型:
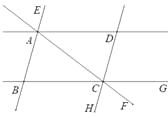
【题目】如图,已知AB∥CD,∠ABC=∠ADC.则下列结论:①BC∥AD;②∠EAC+∠HCF=180°;③若AD平分∠EAC,则CF平分∠HCG;④S四边形ABCD=2S△ABC,其中正确结论的序号是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:早高峰期间,乘坐______(填“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
用时 |
|
|
| 合计(频次) |
线路 | ||||
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
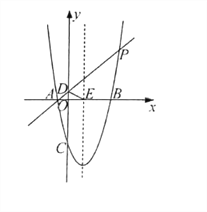
【题目】已知抛物线y=a(x-2)2-9经过点P(6,7),与x轴交于A、B两点,与y轴交于点C,直线AP与y轴交于点D,抛物线对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)过点E任作一条直线l(点B、C分别位于直线l的异侧),设点C到直线的距离为m,点B到直线l的距离为n,求m+n的最大值;
(3)y轴上是否存在点Q,使∠QPD=∠DEO,若存在,请求出点Q的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于 6,△BEF的面积等于4,则四边形CDFE的面积等于___________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com