
 如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似.
如图,正方形ABCD边长是4,P是CD中点,Q是线段BC上一点,当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似. 分析 当Rt△ADP∽Rt△QCP时,$\frac{AD}{QC}$=$\frac{DP}{CP}$;当Rt△ADP∽Rt△PCQ时,$\frac{AD}{PC}$=$\frac{DP}{QC}$;即可求得CQ的长度,即可解题.
解答 解:当Rt△ADP∽Rt△QCP时,有$\frac{AD}{QC}$=$\frac{DP}{CP}$,
即$\frac{4}{QC}$=$\frac{2}{2}$,解得QC=4;
当Rt△ADP∽Rt△PCQ时,$\frac{AD}{PC}$=$\frac{DP}{QC}$,
即$\frac{4}{2}$=$\frac{2}{QC}$,解得QC=1.
故当CQ=4或1时,以由Q,C,P三点为顶点的三角形与△ADP相似,
故答案为:4或1.
点评 本题考查了相似三角形的判定,相似三角形对应边相等的性质,正方形的性质,本题中讨论$\frac{AD}{QC}$=$\frac{DP}{CP}$或$\frac{AD}{PC}$=$\frac{DP}{QC}$是解题的关键.


科目:初中数学 来源: 题型:选择题
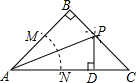 如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:
如图,在等腰直角△ABC中,B=90°,以点A为圆心任意长为半径画弧,与AB,AC分别交于点M,N,分别以点M,N为圆心大于$\frac{1}{2}$MN长为半径画弧,两弧交于点P,且点P刚好落在边BC上,AB=10cm,下列说法中:| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.
如图,在?ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,EF=2$\sqrt{3}$,则AB的长为4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平行四边形的对角线相等 | B. | 矩形的对角线互相垂直 | ||
| C. | 菱形的对角线互相垂直且平分 | D. | 对角线相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,线段AB和射线BM交于点B,利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)
已知:如图,线段AB和射线BM交于点B,利用尺规完成以下作图,并保留作图痕迹.(不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-2,b=1 | B. | a=3,b=-2 | C. | a=0,b=1 | D. | a=2,b=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com