
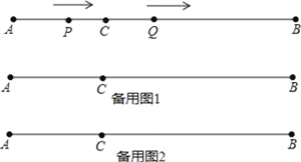
����Ŀ����ͼ��AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC������P�ӵ�A��������3cm/s���ٶ������˶��������B���������أ���3cm/s���ٶ������˶�������Q�ӵ�C��������1cm/s���ٶ������˶���������ͬʱ�������˶�ʱ��Ϊts������P���Q�ڶ����غ�ʱ��P��Q����ֹͣ�˶���
��1��AC=__cm��BC=__cm��
��2����tΪ��ֵʱ��AP=PQ��
��3����tΪ��ֵʱ��PQ=1cm��

���𰸡� 4 8
�������������������1������AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC����AC+BC=3AC=AB=12cm�����˼�����⣻
��2���ֱ��ʾ��AP��PQ��Ȼ����ݵ�����ϵAP=PQ�г�������⼴�ɣ�
��3��������ǰ���������Լ�����B�㷵�غ����1cm��������г�������⼴�ɣ�
�����������1����AB=12cm����C���߶�AB�ϵ�һ�㣬BC=2AC��
��AC+BC=3AC=AB=12cm��
��AC=4cm��BC=8cm��
��2���������֪��AP=3t��PQ=4����3t��t����
��3t=4����3t��t����
��ã�t=![]() ��
��
�𣺵�t=![]() ʱ��AP=PQ��
ʱ��AP=PQ��
��3���ߵ�P��Q����·��Ϊ1cm��
����4+t����3t=1������ǰ����3t����4+t��=1����һ��������
���t=![]() ��t=
��t=![]() ��
��
������B��ʱ����һ���������P��Q����·��Ϊ1cm��
3t+4+t=12+12��1
��ã�t=![]() ��
��
�𣺵�tΪ![]() ��
�� ![]() ��
�� ![]() ʱ��PQ=1cm��
ʱ��PQ=1cm��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
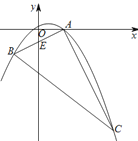
����Ŀ����ͼ��������![]() ��A��1,0����B����1����1����C��3��m�����㡣
��A��1,0����B����1����1����C��3��m�����㡣
��1���������ߵĽ���ʽ��m��ֵ��
��2���ж�![]() ��AC��λ�ù�ϵ����֤����Ľ��ۣ�
��AC��λ�ù�ϵ����֤����Ľ��ۣ�
��3�������������Ƿ���ڵ�P����PH![]() x���ڵ�Hʱ����P��H��AΪ�������������
x���ڵ�Hʱ����P��H��AΪ�������������![]() �����ƣ������ڣ������P���ꣻ�������ڣ���˵�����ɡ�
�����ƣ������ڣ������P���ꣻ�������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС������ÿ����¥��֮�俪���̵أ�������һ�������Ϊ60m2�ij������̵أ����ҳ��ȿ���7m�����εĿ������賤�����̵صĿ�Ϊxm������з���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC��DE��BC�� 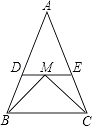
��1�����ʡ�ADE�Ƿ��ǵ��������Σ�˵�����ɣ�
��2����MΪDE�ϵĵ㣬��BMƽ�֡�ABC��CMƽ�֡�ACB������ADE���ܳ�Ϊ20��BC=8�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y����2��x��3��2+4�Ķ��������ǣ�������
A.��3��4��B.����3��4��C.��3����4��D.����3����4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABCDE�У�AB��CD����1����2����3�ֱ��ǡ�BAE����AED����EDC����ǣ����1+��2+��3= �� 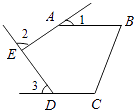
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��MAN=120�㣬ACƽ�֡�MAN��B��D�ֱ�������AN��AM�ϣ� 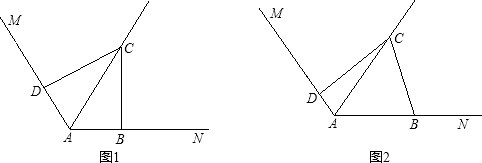
��1����ͼ��1���У�����ABC=��ADC=90��ʱ����֤��AD+AB=AC��
��2�����ѣ�1���е���������ABC=��ADC=90�㡱��Ϊ��ABC+��ADC=180�㣬�����������䣬��ͼ��2����ʾ����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y������x��1��2+3����t��x��4ʱ��y��x���������С����ʵ��t��ȡֵ��Χ�ǣ�������
A.t��0B.0��t��1C.1��t��4D.t��4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com