
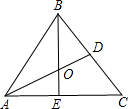
 如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$.
如图,等边三角形的边长为2,中线AD与中线BE相交于点O,则OA2=$\frac{4}{3}$. 分析 根据等边三角形三线合一的特点及直角三角形的性质解答即可.
解答 解:∵△ABC是等边三角形,AD、BE为中线;
∴BD=AE=1,∠ABE=∠BAD=30°,∠AEB=∠ADB=90°;
∴AD=BE=AB•sin60°=$\sqrt{3}$;
在Rt△BOD中,BD=1,∠DBO=30°;
∴OD=BD•tan30°=1×$\frac{\sqrt{3}}{3}$;
∴OA=AD-OD=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$,
∴OA2的长度$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 此题比较简单,解答此题的关键是熟知等边三角形三线合一的性质.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
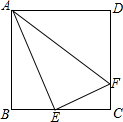 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CD=4CF,下列结论:| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
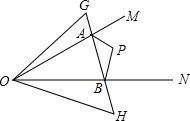 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=80°.
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若∠MON=40°,则∠GOH=80°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com