
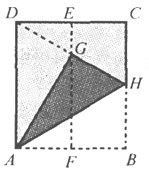
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
【答案】A
【解析】试题分析:先证明EG是△DCH的中位线,继而得出DG=HG,然后证明△ADG≌△AHG,得出∠BAH=∠HAG=∠DAG=30°,在Rt△ABH中,可求出AB,也即是CD的长.
解:∵点E,F分别是CD和AB的中点,
∴EF⊥AB,
∴EF∥BC,
∴EG是△DCH的中位线,
∴DG=HG,
由折叠的性质可得:∠AGH=∠ABH=90°,
∴∠AGH=∠AGD=90°,
在△AGH和△AGD中,
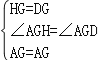 ,
,
∴△ADG≌△AHG(SAS),
∴AD=AH,∠DAG=∠HAG,
由折叠的性质可得:∠BAH=∠HAG,
∴∠BAH=∠HAG=∠DAG=![]() ∠BAD=30°,
∠BAD=30°,
在Rt△ABH中,AH=AD=4,∠BAH=30°,
∴HB=2,AB=2![]() ,
,
∴CD=AB=2![]() .
.
故选:B.


科目:初中数学 来源: 题型:
【题目】点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm、PB=5cm、PC=2cm,则点P到直线l的距离( )
A.等于4cm
B.等于2cm
C.小于2cm
D.不大于2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
⑴画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
⑵画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
⑶在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:

(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.


(1)(4分)求证:△AOD≌△EOC;
(2)(5分)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=120![]() ,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )
,BC=6cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为( )

A. 1.5cm B. 2cm C. 2.5cm D. 3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com